Multilevel Modeling (LT5)
Preliminaries
library(jtools)
library(interactions)
library(ggplot2)
library(tidyverse)
library(lme4)
library(readr)The Scourge of Data Dependence
As we saw in LT1, when we run tests using the GLM we make several assumptions. Some, like normality of residuals and linearity, we can test for. But some, like perfect measurement and independence, we cannot.
We have seen in the past few weeks how we can solve the issue of measurement error on estimates by test relationships using latent variables. However, this leaves one tricky assumption left to deal with: independence. That is, all observations in your data are independent of each other.
The assumption of independence is used for all GLM tests. It’s essential to getting results from your sample that reflect what you would find in a population. Even the smallest dependence in your data can turn into heavily biased results (which may be undetectable) if you violate this assumption.
A dependence is a connection between your data. For example, it could be that workers at tech companies are more responsive to incentives than workers on care homes. If aggregate all tech and care workers and test the relationship between incentives and performance the estimates will be biased.
In simple terms, if you violate the assumption of independence, you run the risk that all of your results will be wrong. And this is a major problem because in the real world, how can we really be sure there are no dependencies in our data? There are dependencies EVERYWHERE. People within countries, people within regions within countries. Children within schools, children within local authorities within schools. Adults within workplaces, adults within sectors within workplaces. We could go on.. The possibilities are endless.
And it isn’t just unit clustering that can be a problem. What about when we collect longitudinal data? It is not likely that the observations taken over multiple time points from a single subject are independent. If a subject begins a study with a relatively high level of anxiety, for example, chances are good that they will have relatively high anxiety levels throughout the study. So observations can cluster within people, just as they can within units of measurement.
We therefore need someway of accounting for the potential dependency in our data.
Multilevel Modeling
Multilevel models (MLMs, also known as linear mixed models, hierarchical linear models or mixed-effect models) have become increasingly popular in psychology for analyzing data with repeated measurements or data organized in nested levels (e.g., students in classrooms). Although mathematically sophisticated, MLMs are easy to use once familiar with some basic concepts.
Lets begin with what we do know. In the GLM, we have been modeling data using the following formula:
yi ~ a + B*Xi + ei
For each case, the outcome or “y” score can be separated into fixed and random effects. The fixed effects include the intercept (a) and the slope (B) for the independent variable “X.” These are considered fixed because they take on set values (i.e., the mean intercept of all possible intercepts and the mean slope of all possible slopes).

Fixed Effects in a GLM
The general error term (ei) captures the error in prediction for case i. This error term can be considered “random” because we assume there is some person to person variation (residual) that cannot be accounted for by the fixed effects. We estimate the variance of this error term to find our standard error.
The issue with this fixed approach is that if, for example, we recruited children from different schools, then we violate the GLM assumption that observations are independent from each other. We would have different intercepts and different slopes for each school.
In other words, observations from the same school are likely to be “clustered,” and a MLM adds some extra parameters that control for this clustering. In particular, MLMs add structure to the error term (ei) from the GLM. Instead of one general random-effect that captures how each observation deviates from the predicted fixed-effects, there will be multiple random-effects that capture how intercepts and slopes deviate within a cluster, and how each cluster deviates from the overall group.

Random Effects in MLM
Lets say we are interested in the relationship between time doing homework and math gpa with data that is clustered within schools. The basic MLM with random intercepts and slopes takes the following form at level 1:
mathij = aj + Bj*homeworkij + eij
Where i means student and j means school (our clustering unit). a and B are, as always, the intercept and slope. e is the error term.
Here we have specified that the intercepts and slopes vary by school (i.e., subscript j). As such, we need to include two level 2 models for the random intercepts and random slopes:
aj = Ma + Waj
Bj = MB + WBj
Where Ma and MB are the fixed intercept and slope values and Waj and WBj are the random error components for the intercepts and slopes (i.e., the deviation of group j from the fixed effect). The presence of WBj in the model is what allows the effect of homework to vary across schools.
Yielding the following combined (mixed) equation:
mathij = Ma + (MB + WBj)*homeworkij + Waj + eij
In MLM, coefficients are tested for significance against zero, and in this model, the significance test of the mean slope (is the mean slope significantly different from zero?) is made at Level 2, via the MB coefficient. If the MB coefficient is significantly different from zero, then the null hypothesis is rejected.
The intercept is also tested for significance via the Ma coefficient. That is, is the mean intercept significantly different from zero? The meaning of these tests, that is, what the coefficients represent, will vary as a function of the measures themselves, and most important, the meaning of the intercept will vary as a function of how the Level-1 predictors are centered, a topic we will discuss below.
In MLM, the random error terms for Level-1 coefficients (the deviations of the group mean intercepts and slopes from the overall mean intercepts and slopes, signified by Waj and WBj) are also tested for significance, and such significance tests can be used to make decisions about including or excluding random error terms from models.
When an error term for a coefficient is included in a model, the coefficient is referred to as a random effect (because it is allowed to vary randomly). When an error term is not included, the coefficient is referred to as a fixed effect (because it is not allowed to vary). Fixed effects are analogous to the coefficients yielded in normal regression.
There are two main types of clustering: clustering within units and clustering within persons. let’s begin by looking at clustering within units.
Cross-Sectional Data: People Nested Within Units
Data nested within units is a special type of data where there is only one measurement per participant (i.e., there is no within subject variable), and participants are nested in units (e.g., workplaces, schools, etc) so we must control for the clustering effects of these units when we calculate statistical estimates
Let’s take a look at a simple example with this type of nested data.
We have six schools in our local area. Three of these are in rich catchment areas and three are in poor catchment areas. There are 40 students in each rich school and there are 160 students in each poor school.
We wanted to know whether student happiness can be predicted by the number of friends they have. So we measured them on Happiness, number of Friends. For good measure, we also took their GPA.
If we ran an linear regression of happiness on friends in the total dataset, we run the risk of missing potentially important clustering effects in this data. That is, given the specific characteristics of our schools, it is likely that the impact of friends on happiness will be different from school to school. Perhaps the impact of friends on happiness is greater in the poor schools than it is in the rich schools. This is a classic cse of clustering. We need to add the appropriate random effects of schools to our regression model.
In this study our Level 1 will be the lowest unit of observation - those nested in groups. In this case, Level 1 is the students.
Our Level 2 refers to the groups in which the level 1 units are nested; in this case Level 2 is the schools.

A Two-Level Nested Unit Data-Structure
The Data
As always, let’s first load in the school data here:
library(psych)##
## Attaching package: 'psych'## The following objects are masked from 'package:ggplot2':
##
## %+%, alphaschool <- read_csv("C:/Users/CURRANT/Dropbox/Work/LSE/PB230/LT5/Workshop/school.csv")##
## -- Column specification --------------------------------------------
## cols(
## happy = col_double(),
## friend = col_double(),
## gpa = col_double(),
## id = col_double(),
## school = col_double()
## )head(school)## # A tibble: 6 x 5
## happy friend gpa id school
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 38.7 0 3.79 401 5
## 2 46.3 0 1.15 565 6
## 3 51.7 0 1.09 547 6
## 4 60.6 0 2.75 377 5
## 5 55.1 0 2.72 335 5
## 6 29.4 0 3.92 325 5describe(school)## vars n mean sd median trimmed mad min max range skew
## happy 1 600 70.68 16.13 69.88 70.31 16.46 29.36 126.32 96.96 0.23
## friend 2 600 5.89 2.77 5.00 5.69 2.97 0.00 15.00 15.00 0.66
## gpa 3 600 2.45 0.90 2.46 2.45 1.20 1.00 4.00 3.00 0.06
## id 4 600 300.50 173.35 300.50 300.50 222.39 1.00 600.00 599.00 0.00
## school 5 600 4.40 1.45 5.00 4.58 1.48 1.00 6.00 5.00 -0.85
## kurtosis se
## happy 0.08 0.66
## friend 0.30 0.11
## gpa -1.25 0.04
## id -1.21 7.08
## school -0.04 0.06You will see that data contains measures for our variables:
happy: This is the happiness measure, which can range from 0 to 130. It is an aggregate score from multiple measures and higher values mean higher happiness.
friends: This is friends measure and can range from 0 to infinity but in reality it ranges from 0 to 15. Higher values mean more friends.
gpa: This is the gpa variable. Higher values mean higher grades.
id: This is the unique student id number for level 1 units.
school: This is the unique school identifier for level 2 units.
The 2 Level Multilevel Model for Unit Clustering
The research question is interested in whether students with more friends are happier than students with less friends. Based on our knowledge of happiness theory we would hypothesize that there should be a positive relationship between these variables.
Note that we cannot test this question using the GLM. The relationships may be nested within schools, or at least we have nesting in this data that we cannot ignore lest we wish to violate the assumption if independence. We need to account for this nesting by estimates random effects of intercepts and slopes using MLM.
To visualize the relationships across the schools in our data set, lets first plot the within-school relationships between friends and happiness. To do this, we just plot friends against happiness and group the plots by school:
ggplot(data = school, aes(x = friend, y=happy,group=school))+
facet_grid( ~ school)+
geom_point(aes(colour = school))+
geom_smooth(method = "lm", se = TRUE, aes(colour = school))+ xlab("Friends")+ylab("Happiness")+
theme(legend.position = "none") ## `geom_smooth()` using formula 'y ~ x'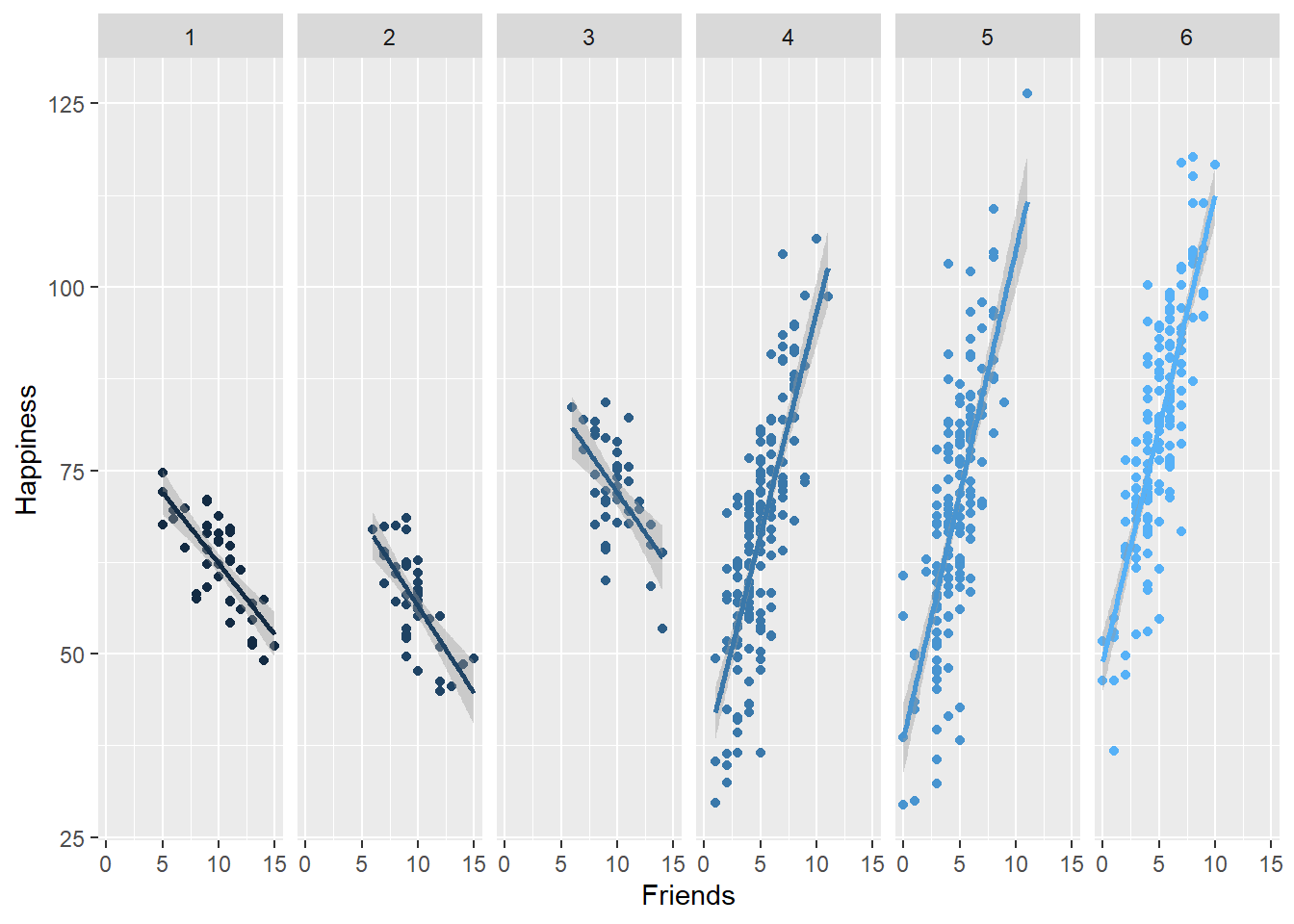
Let’s see what our correlation looks like when lumping all the rich and poor schools together.
cor(school[,1:2])## happy friend
## happy 1.0000000 0.2383908
## friend 0.2383908 1.0000000Notice how the correlation between Friends and Happiness in the overall sample is positive (.24) but the scatter plots show substantial between-school variability in this correlation? It is a positive correlation, but as we can see in the data, only poor schools (those with loads more students) had a positive correlation. We have a problem in estimation that needs solving with MLM.
Regular Regression
Let’s try running a normal regression on all the data at once, just to show why the assumption of independence is so important.
First, though, let’s center the predictor variable so that the intercept in our model has the interpretation of the mean friend score.
school$friend.c <- school$friend - mean(school$friend) Now we can run the regression:
lm.model <- lm(happy ~ friend.c, data = school)
summary(lm.model)##
## Call:
## lm(formula = happy ~ friend.c, data = school)
##
## Residuals:
## Min 1Q Median 3Q Max
## -34.960 -10.829 -0.298 10.920 48.543
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 70.684 0.640 110.440 < 2e-16 ***
## friend.c 1.387 0.231 6.003 3.37e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.68 on 598 degrees of freedom
## Multiple R-squared: 0.05683, Adjusted R-squared: 0.05525
## F-statistic: 36.03 on 1 and 598 DF, p-value: 3.367e-09Putting all schools together in a regular regression, we have a positive, significant effect of Friends. But what happens when we separate the schools by rich or poor status?
For this we run a normal regression on rich and poor schools separately:
# Rich Schools
School.Rich.Reg.Model <- lm(happy ~ friend.c, data = subset(school, school<4))
summary(School.Rich.Reg.Model)##
## Call:
## lm(formula = happy ~ friend.c, data = subset(school, school <
## 4))
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.122 -5.894 -1.214 5.372 20.490
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 72.0011 1.5504 46.439 < 2e-16 ***
## friend.c -2.0237 0.3479 -5.817 5.23e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.009 on 118 degrees of freedom
## Multiple R-squared: 0.2229, Adjusted R-squared: 0.2163
## F-statistic: 33.84 on 1 and 118 DF, p-value: 5.235e-08# Poor Schools
School.Poor.Reg.Model <- lm(happy ~ friend.c, data = subset(school, school>3))
summary(School.Poor.Reg.Model)##
## Call:
## lm(formula = happy ~ friend.c, data = subset(school, school >
## 3))
##
## Residuals:
## Min 1Q Median 3Q Max
## -36.496 -7.790 0.543 7.839 36.607
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 78.6995 0.6026 130.60 <2e-16 ***
## friend.c 6.4692 0.2801 23.09 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.74 on 478 degrees of freedom
## Multiple R-squared: 0.5273, Adjusted R-squared: 0.5264
## F-statistic: 533.3 on 1 and 478 DF, p-value: < 2.2e-16Notice, we have a negative, significant effect for Friends in the rich schools but a positive, significant effect of Friends in the poor school. Thats no good!
Whats the Problem?
Remember! Although I am telling you that some schools are rich and some are poor, you may not know this information when you come in and try to do the analysis.
The regular regression did not reflect what was happening in each school type. It gave us a positive effect (Friends) when only poor schools had a positive effect. Collapsing across school types in this case was not ideal because different things were happening within each school type, compromising the generalizability of the findings.
Another way to put this, the regular (lm) regression indicates that the more friends a student has, the happier they are, but looking closer this is not the case in all schools (and is, in fact, the opposite in some). If you were trying to generalize your findings or use them to argue for/show a need for an intervention, your results would be misleading and could cause problems.
So, let’s try running this as a multilevel model instead and capture the school to school variability with random effects.
Setting up the 2-Level Multilevel Model for Unit Clustering
We are interested in the relationship between happiness and friends with data that is clustered within schools. We know this because we have just seen this clustering in action!
The basic MLM capturing this clustering with random intercepts and slopes takes the following form at level 1:
happinessij = aj + Bj*friendsij + eij
Where i means student and j means school (our clustering unit). a and B are, as always, the intercept and slope. e is the error term.
Here we have specified that the intercepts and slopes vary by school (i.e., subscript j). As such, we need to include two level 2 models for the random intercepts and random slopes:
aj = Ma + Waj
Bj = MB + WBj
Where Ma and MB are the fixed intercept and slope values and Waj and WBj are the random error components for the intercepts and slopes (i.e., the deviation of group j from the fixed, average, effect). The presence of WBj in the model is what allows the effect of friends to vary across schools (i.e., to be different for each school).
Pulling this together we get the following combined (mixed) equation:
happinessij = Ma + (MB + WBj)*friendsij + Waj + eij
Put simply, using a multilevel model allows us to separate the within-school effects from the between-school effects, whereas regular regression blends them together into a single coefficient.
The Empty Model
The first thing we do in multilevel modeling is check whether there is indeed between-cluster variance in the outcome variable. We do this with the intraclass correlation coefficient which is calculated using the between-group and residual variance from an empty model of happiness.
To run a multilevel linear model, we use the lmer() function (“Linear Mixed Effects in R”) from the lme4 package. The syntax will look very similar to the syntax from all of the regression functions we have used thus far. Fitting the empty model for happiness looks like this:
empty.happiness.fit <- lmer(formula = happy ~ 1 + (1|school), data=school, REML=FALSE)
summary(empty.happiness.fit)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: happy ~ 1 + (1 | school)
## Data: school
##
## AIC BIC logLik deviance df.resid
## 4933.3 4946.5 -2463.7 4927.3 597
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.0540 -0.6053 0.0226 0.6014 3.9123
##
## Random effects:
## Groups Name Variance Std.Dev.
## school (Intercept) 54.56 7.387
## Residual 209.21 14.464
## Number of obs: 600, groups: school, 6
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 68.336 3.103 22.02Note that R uses restricted maximum likelihood to fit the model. If you turn this off with the REML=FALSE option (as I have done), it will use the minimization of the log-likelihood instead to fit the model, which aligns with what we did last year in logistic regression.
In this model, the code for the model reads, “happy ~ 1 + (1|school).” The “1|school” section of the model is specified in order to only estimate 1 intercept for happiness and to group the data by school “|”. This intercept represents the mean happiness score across all participants over all schools. In this way, we calculate the deviation of each school mean from the overall mean (intercept) for between-school variance.
The variance component, 54.56, tells us how much between-school variance there is in happiness (i.e., variability in happiness from school to school).
The residual section reads 209.21, and represents the variability that is left unexplained in the empty model after the variance attributable to school has been subtracted out (much like the error variance in an ANOVA model). This left over variance is the between-pupil variance (i.e., variability in happiness from person to person over all schools)
To partition the variance into between-school and between-pupil sources, we take the variance component of the intercept and divide it by the sum of the residual variance and the intercept variance. This is the calculation for the ICC we saw in the lecture:
ICC = σbg2 / (σbg2 + σerror2) or variance between schools / total variance
This leaves us with: 54.56 / (54.56 + 209.21) = 0.21. We can calculate this in R:
54.56/(54.56+209.21)## [1] 0.2068469This means that 21 percent of the variance in happiness is due to between-school differences. That’s a lot! This is most definitely a MLM problem.
Adding the Level 2 Predictor Variable to the Empty Model
OK - let’s add the Level 2 predictor of friends to see whether it can explain the within-person variance in happiness. Recall that friends in this data was measured using the centered friend.c variable. We can also get bootstrap confidence intervals for the fixed and random effects for statistical inference using confint().
# fit model
friend.happy.fit <- lmer(formula = happy ~ 1 + friend.c + (1 + friend.c|school), REML=FALSE, data=school)
summary(friend.happy.fit)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: happy ~ 1 + friend.c + (1 + friend.c | school)
## Data: school
##
## AIC BIC logLik deviance df.resid
## 4444.4 4470.7 -2216.2 4432.4 594
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.5964 -0.5755 0.0362 0.6422 4.0411
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## school (Intercept) 42.32 6.505
## friend.c 17.75 4.213 0.53
## Residual 87.57 9.358
## Number of obs: 600, groups: school, 6
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 75.250 2.796 26.913
## friend.c 2.153 1.734 1.241
##
## Correlation of Fixed Effects:
## (Intr)
## friend.c 0.471confint(friend.happy.fit, method="boot", nsim=100)## Computing bootstrap confidence intervals ...##
## 7 message(s): boundary (singular) fit: see ?isSingular
## 1 warning(s): NA values in sdcor matrix converted to 0## 2.5 % 97.5 %
## .sig01 1.4934124 9.317330
## .sig02 -0.5189012 1.000000
## .sig03 1.5722873 5.664174
## .sigma 8.7381177 9.925323
## (Intercept) 69.3989776 82.114798
## friend.c -1.0320752 6.097700The “1 + friend.c|school” portion of this equation is requesting that both the intercepts “1” and slope of friends “friend.c” are allowed to vary randomly across schools “|school”.
This output needs some explaining.
Fixed Effects (mean of the random intercepts and slopes):
(Intercept): The expected value of happiness for the average student with the average number of friends is 75.25
friend.c: For every unit increase in friend, happiness increased by 2.15. To know whether this fixed effect is significantly greater than zero, we inspect friend.c from the confidence interval table. We can see that the 95% CI includes zero (95% Ci = -1.84,5.41). This not a significant relationship.
Random Effects (variability of random intercepts and slopes):
sd((Intercept)): There is between-school variability in the intercepts of happiness (variance = 42.32, sd = 6.51). To know whether this variability is significantly greater than zero, we inspect sig01 from the confidence interval table. We can see that the standardised variance of the intercepts (i.e., the SD) is 6.51 with a 95% CI from 1.73 to 10.07. This does not include zero. So even though the intercept variance is reduced with the addition of friends to the empty model, there is still a significant amount of random variance in the intercepts to be explained.
sd(friend.c): There is between-school variability in the slopes of happiness on friends (variance = 17.75, sd = 4.21). In other words, there is substantial variance in the slopes of happiness on friends from school to school (but we already know this!).
To know whether this school to school variability in the slopes of happiness on friends is significantly greater than zero, we inspect sig03 from the confidence interval table. We can see that the standardised variance of the slopes (i.e., the SD) is 4.21 with a 95% CI from 1.37 to 6.71. This does not include zero. There is a significant amount of random variance in the slopes.
- cov((Intercept),friend.c: The correlation between the random intercept and random slope was 0.53, which indicates that those schools who had higher intercepts for happiness were also likely to have greater associations between friends and happiness. To know whether this correlation is significantly greater than zero, we inspect sig02 from the confidence interval table. We can see that the relationship between the intercepts and slopes is not significant (95% CI = - 33,1.00).
We can plot the within-school happiness slopes and intercepts to get a sense of the school to school variability in this data:
ggplot(data=school, aes(x=friend.c, y=happy, group=factor(school), colour="gray"), legend=FALSE) +
geom_smooth(method=lm, se=FALSE, fullrange=FALSE, lty=1, size=.5, color="gray40") +
geom_smooth(aes(group=1), method=lm, se=FALSE, fullrange=FALSE, lty=1, size=1, color="blue") +
xlab("Grand Mean Centered Friends") + ylab("Happiness") +
theme_classic(base_size = 8) +
theme(axis.title=element_text(size=18),
axis.text=element_text(size=14),
plot.title=element_text(size=18, hjust=.5)) +
ggtitle("Within-School Effect of Friends on Happiness")+
geom_vline(xintercept=0)## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'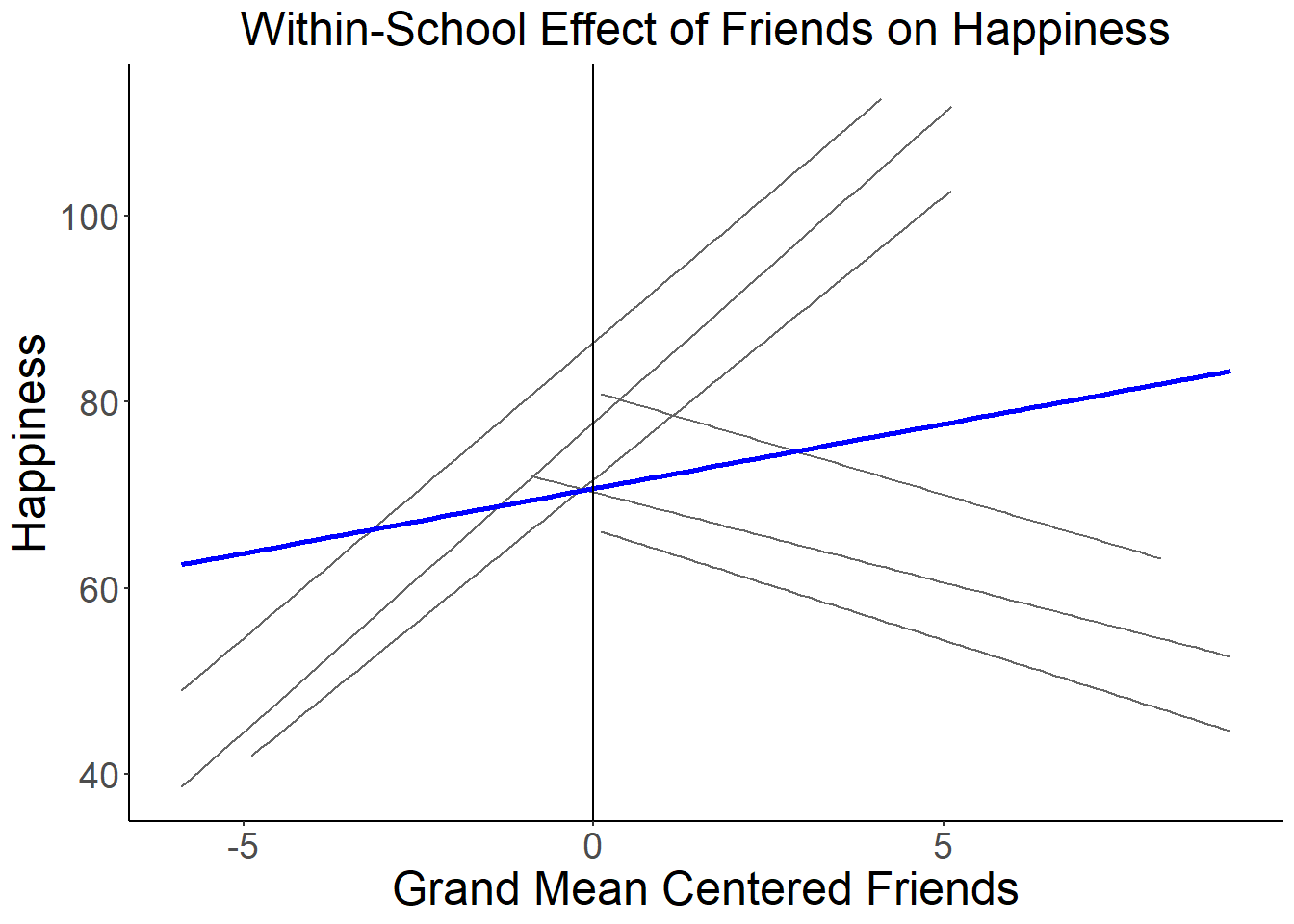
The blue line here shows the fixed intercept (i.e., where the fixed slope line crosses zero) and fixed slope of stress on time (i.e., the mean of the random slopes). As we saw from the MLM output, the fixed slope is not significant even though it is a fairly large positive correlation. It is not significant, of course, because there is substantial variability between schools in relationships between friends and happiness as we can see in the individual slopes for each school.
What Does This All Mean?
In our regular (lm) regression, Friends had a significant effect on happiness, b = 1.39 (p < .001). However, in our mixed (lmer) regression, Friends had a larger (2.15), but non-significant effect.
Why is this important? The goal of multilevel modeling is to draw a conclusion about the general sample that you have while controlling for differences you are not trying to explain (in this example, rich vs. poor). Not properly controlling for these differences, which you may often not know are there, will increase your chance of Type I error.
Because the effect of Friends was different in different schools, it makes sense that the multilevel model (MLM) did not show a significant effect. In the present example, our MLM gave us a more accurate interpretation: that no main effect of Friends existed for all schools generally.
I hope it is clear now why this analysis matters!
How its Written
The intraclass correlation for happiness was first calculated based on the empty model. This was to determine whether the Level 1 outcome (i.e. happiness) had substantial between-school variation (Model 1). The intraclass correlation of happiness was .21, indicating substantial between-school variance.
In model 2, we added fixed and random effects for the happiness intercepts and friend slopes on happiness to model 1. With 5000 bootstrap resamples, the fixed effect of friends on happiness was not different from zero with these random effects in the model (b = 2.19, 95% CI = -1.84,5.41). Therefore, the MLM showed that friends does not correlate with happiness over all schools.
Longitudinal Data: Time Points Nested Within People
Another application of multilevel modeling, as we saw in the lecture, is for longitudinal data where time points are nested within people.
The data we are going to work with for the analysis of longitudinal data is the stress data from Ram et al (2012). This is a classic diary design, whereby the researchers were interested to know the effects of personalty of daily levels of stress. The citation for the work is here:
Ram, N., Conroy, D. E., Pincus, A. L., Hyde, A. L., & Molloy, L. E. (2012). Tethering theory to method: Using measures of intraindividual variability to operationalize individuals’ dynamic characteristics. In G. Hancock & J. Harring (Eds.), Advances in longitudinal methods in the social and behavioral sciences (pp. 81-110). New York: Information Age.
As we saw in the lecture, longitudinal data is a special case of nested data where time points are nested within people. In this case, the data Ram collected was from a diary study of workers in a big tech firm. Once a day for eight days, researchers measured employees’ levels of stress and negative affect (this is why it is called a diary study, participants typically complete a daily diary).
At the end of the study, they took one measure of neuroticism. In this way, the researchers have data at two-levels. At level two, they had between person differences in neuroticism (i.e., how people differ from the sample mean in terms of their neuroticism). At level one, they had within-person differences in stress and negative affect (i.e., how people differ from their own mean stress and negative affect on a particular day).

A Two-Level Nested Longitudinal Data-Structure
The researchers were interested to know whether neuroticism in the workplace had a couple of functions:
Does neuroticism predict the change trajectories of stress over the period of study? To address this question we need to examine the interaction of time and neuroticism on stress.
Does neuroticism predict stress reactivity? To address this question we need to examine the interaction of stress and neuroticism on negative affect.
The Data
As always, let’s first load in the data here:
stress <- read_csv("C:/Users/CURRANT/Dropbox/Work/LSE/PB230/LT5/Workshop/stress.csv")##
## -- Column specification --------------------------------------------
## cols(
## id = col_double(),
## day = col_double(),
## negaff = col_double(),
## stress = col_double(),
## neurotic = col_double(),
## stress_personmean = col_double(),
## negaff_personmean = col_double(),
## neurotic_gmc = col_double(),
## stress_gmc = col_double(),
## stress_pmc = col_double(),
## negaff_pmc = col_double()
## )head(stress, 16)## # A tibble: 16 x 11
## id day negaff stress neurotic stress_personme~ negaff_personme~
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 101 0 3 1.5 2 1.06 1.5
## 2 101 1 2.3 1.25 2 1.06 1.5
## 3 101 2 1 0.5 2 1.06 1.5
## 4 101 3 1.3 1 2 1.06 1.5
## 5 101 4 1.1 1.25 2 1.06 1.5
## 6 101 5 1 1.25 2 1.06 1.5
## 7 101 6 1.2 0.5 2 1.06 1.5
## 8 101 7 1.1 1.25 2 1.06 1.5
## 9 102 0 1.4 0.5 2 0.781 2.22
## 10 102 1 1.6 0 2 0.781 2.22
## 11 102 2 2.6 0 2 0.781 2.22
## 12 102 3 2.8 2.25 2 0.781 2.22
## 13 102 4 1.7 0 2 0.781 2.22
## 14 102 5 2.65 0.25 2 0.781 2.22
## 15 102 6 2.2 1.25 2 0.781 2.22
## 16 102 7 2.8 2 2 0.781 2.22
## # ... with 4 more variables: neurotic_gmc <dbl>, stress_gmc <dbl>,
## # stress_pmc <dbl>, negaff_pmc <dbl>You will see that this data is structured longways, just like last year in within-person factorial ANOVA, with the time points represented by a new row in the data. The variables are in various states of preparedness, so it is important to quickly give an overview of what each variable is measuring.
id: This is the ID variable for each participant in the study. There are eight days worth of data for each participant so there are eight rows for each id.
day: This is the time variable that here reflects the day of measurement. With longitudinal data in MLM, it is important to center the time variable at 0 for the first measurement occasion so that intercepts in MLM models reflect the first time point.
negaff: This is the score for negative affect given by each participant at each measurement occasion. The negative affect measure runs from 1 to 7 with higher scores indicating higher negative affect on that day.
stress: This is the score for stress given by each participant at each measurement occasion. The stress measure runs from 1 to 4 with higher scores indicating higher stress on that day.
neurotic: This is the score for neuroticism given by each participant at the end of the study. The same score is repeated for all eight days in the diary design because neuroticism is a trait and does not fluctuate day-to-day. As such, it is a between-person variable, assumed to be the same at each measurement occasion.
stress_personmean: This is the mean of the daily scores for stress for each participant
negaff_personmean: This is the mean of the daily scores for negative affect for each participant
neurotic_gmc: This is the grand mean centered neuroticism variable. Scores represent deviations of each person’s neuroticism score from the overall sample neuroticism mean.
stress_gmc: This is the grand mean centered stress variable. Scores represent deviations of each person’s mean stress score from the overall sample stress mean.
stress_pmc: This is the person mean centered stress variable. Scores represent deviations of each person’s stress score on a particular day from their mean stress score across all days (i.e., stress_personmean - stress). Positive values mean more stress than average on that particular day, negative values mean less stress than average on that particular day.
negaff_pmc: This is the person mean centered negative affect variable. Scores represent deviations of each person’s negative affect score on a particular day from their mean negative score across all days (i.e., negaff_personmean - negaff). Positive values mean more negative than average on that particular day, negative values mean less negative than average on that particular day.
Setting up the 2-Level Multilevel Model for Change Trajectories
The first research question is interested in whether neurotics have especially steep increases in stress across the period of study. Based on our knowledge of personality theory and the anxious disposition of neurotics, we would hypothesize that neurotics should indeed show steeper increases in stress from the start of the dairy study to the end.
Note that we cannot test this question using the GLM. The trajectories of stress are nested within individuals and so the average effect of time on stress across all people is useless - our hypothesis is that different people will have different trajectories. Just like in the school example above, we need to account for this nesting using MLM.
To visualize the trajectories of stress, lets first plot the within-person relationship between time and stress for a subset of individuals. To do this, we just plot day against the person mean centered stress variable:
#faceted plot
ggplot(data=stress[which(stress$id <= 130),], aes(x=day,y=stress_pmc)) +
geom_point() +
stat_smooth(method="lm", fullrange=TRUE) +
xlab("Time") + ylab("Daily Stress") +
facet_wrap( ~ id) +
theme(axis.title=element_text(size=16),
axis.text=element_text(size=14),
strip.text=element_text(size=14))## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 3 rows containing non-finite values (stat_smooth).## Warning in qt((1 - level)/2, df): NaNs produced## Warning: Removed 3 rows containing missing values (geom_point).## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -
## Inf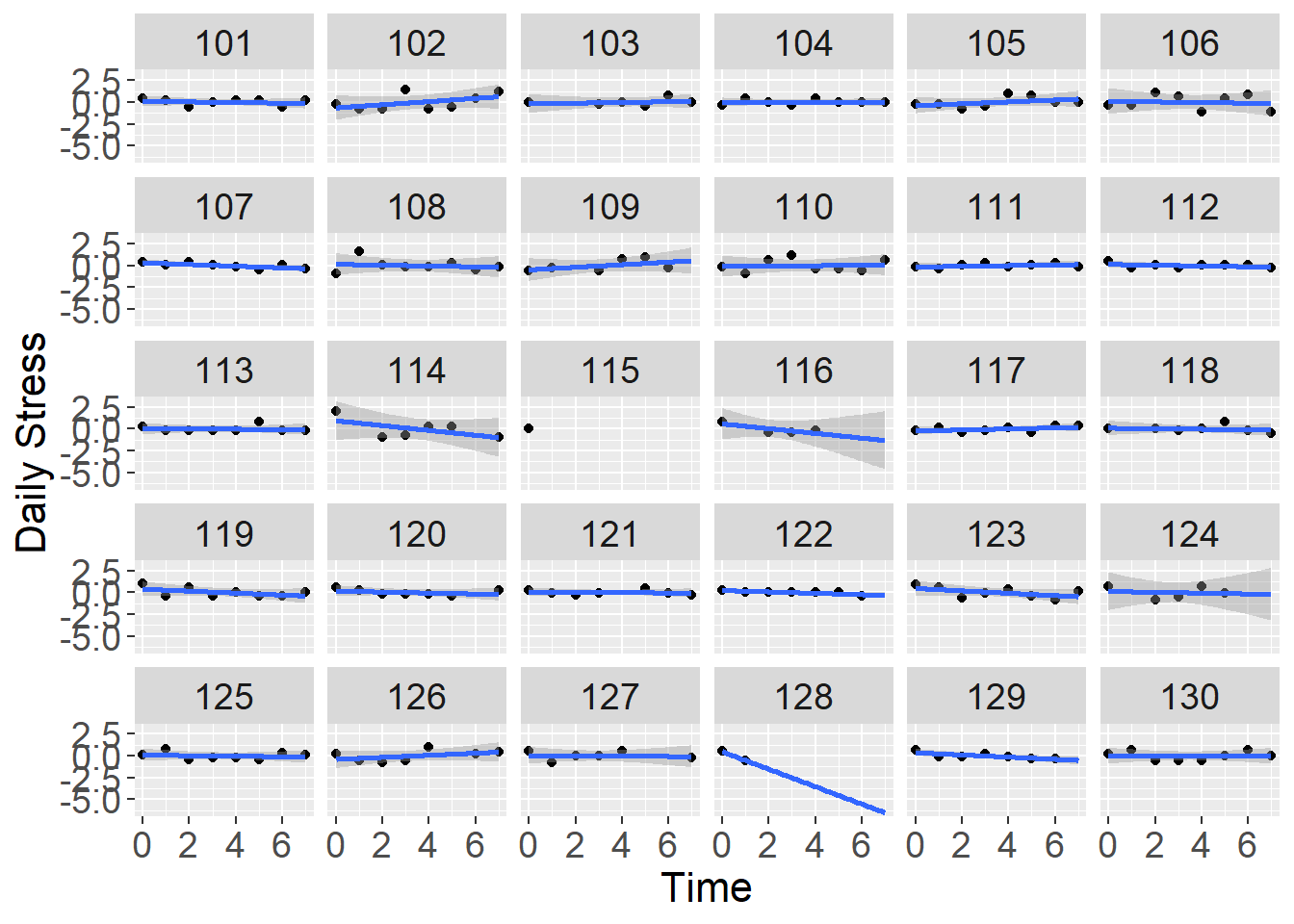
From the panel of plots we get a sense that individuals’ stress scores are generally flat across the diary period, but each person has a slightly different profile of change (trajectory). These differences in change are indicated by differences in the slope of the regression line for stress on our day variable (time).
Our substantive interest is describing within-person differences in stress trajectories and determining if those differences are related to between-person differences in neuroticism.
The basic Level 1 multilevel model is written as:
stressti = ai + Bi*(dayti) + eti
where the time-varying outcome variable (varying from day to day), stressti (stress for person i at time point t) is modeled as a function of a within-person intercept, ai (first time point stress score for person i); a within-person slope, Bi (the stress trajectory for person i); and residual error, eti (the difference between the model predicted stress score for person i at time t and the actual stress score for person i at time t).
The Level 2 random intercepts (ai) are modeled as:
ai = Ma + Ba(neurotici) + Wai
where the intercept for person i, ai (the stress score for person i at the first time point) is modeled as a function of a fixed effect Ma, which describes the mean intercept value across the sample; Ba, which is the relationship of the random stress intercepts with neuroticism (i.e., do those with higher neuroticism start the study with higher stress?). The random effect Wai is the residual unexplained intercept variance not explained by neuroticism (the difference between the model predicted stress intercept for person i and the actual stress intercept for person i).
The Level 2 random slopes (Bi) are modeled as:
Bi = MB + BB(neurotici) + WBi
where the slope for person i, Bi (the stress trajectory for person i) is modeled as a function of a fixed effect MB, which describes the mean stress trajectory across the sample; BB, which is the relationship of the random stress trajectory with neuroticism. The random effect WBi is the residual unexplained stress trajectory not explained by neuroticism (the difference between the model predicted stress trajectory for person i and the actual stress trajectory for person i).
Combining Level 1 and Level 2 equations gives us:
stressti = Ma + (MB + WBi)dayti + Ba(neurotici) + BB(daytineurotici) + Wai + eti
Note the difference between this model and the school model is that we are interested in whether the level 1 stress trajectories are different depending on the level 2 variable: neuroticism. Therefore, we have a cross-level interaction in the model that tests this hypothesis.
Fitting the Empty Model
Now that we have defined the stress trajectory model we can begin to fit it using the multilevel model.
As before, we make use of the lme4 package for fitting such multilevel models. The lmer() function fits the MLM.
Like in the school example above, we often first fit an empty model that provides us information about how much of the total variance in the outcome variable is between-person variance and how much is between-day variance.
Fitting the empty model for stress looks like this:
empty.stress.fit <- lmer(formula = stress ~ 1 + (1|id), data=stress, REML=FALSE)
summary(empty.stress.fit)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: stress ~ 1 + (1 | id)
## Data: stress
##
## AIC BIC logLik deviance df.resid
## 2611.8 2627.6 -1302.9 2605.8 1442
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1923 -0.6625 -0.0665 0.5535 4.0770
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.1857 0.4310
## Residual 0.2812 0.5303
## Number of obs: 1445, groups: id, 190
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 1.3916 0.0344 40.45In this model, the code for the model reads, “stress ~ 1 + (1|id).” The “1|id” section of the model is specified in order to only estimate 1 intercept for stress and group the data “|” by person. This intercept represents the mean stress score across all participants. The variance component, 0.19, tells us how much between-person variance there is in stress (i.e., variability in stress from person to person).
The residual section reads .28, and represents the variability that is left unexplained in the empty model (much like the error variance in an ANOVA model). This left over variance is the between-day variance (i.e., variability in stress from day to day, irrespective of person)
To partition the variance into between-person and between-day sources, we take the variance component of the intercept and divide it by the sum of the residual variance and the intercept variance.
This leaves us with: .19 / (.19 + .28) = 0.40. We can calculate this in R:
.19/(.19+.28)## [1] 0.4042553This means that 40 percent of the variance in stress is due to between-person differences. That’s a lot!
This means there is a good portion of person to person stress variance to be explained by time.
Using the Mutlilevel Model to Examine Between-Person Differences in Within-Person Trajectories of Stress
OK - let’s add the Level 1 predictor of time to see whether it can explain the within-person variance in stress. When we regress stress on time, what we are really doing is testing the trajectories of stress for each participant.
Recall that time in this data was measured using the day variable. We can also get bootstrap confidence intervals for the fixed and random effects for statistical inference using confint().
# fit model
time.stress.fit <- lmer(formula = stress ~ 1 + day + (1 + day|id), REML=FALSE, data=stress)## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.00345471 (tol = 0.002, component 1)summary(time.stress.fit)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: stress ~ 1 + day + (1 + day | id)
## Data: stress
##
## AIC BIC logLik deviance df.resid
## 2602.4 2634.1 -1295.2 2590.4 1439
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1112 -0.6479 -0.0737 0.5605 3.9987
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## id (Intercept) 0.174765 0.41805
## day 0.002812 0.05303 -0.14
## Residual 0.264434 0.51423
## Number of obs: 1445, groups: id, 190
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 1.386688 0.039095 35.470
## day 0.001260 0.007091 0.178
##
## Correlation of Fixed Effects:
## (Intr)
## day -0.493
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00345471 (tol = 0.002, component 1)confint(time.stress.fit, method="boot", nsim=100)## Computing bootstrap confidence intervals ...##
## 2 warning(s): Model failed to converge with max|grad| = 0.00203554 (tol = 0.002, component 1) (and others)## 2.5 % 97.5 %
## .sig01 0.35181807 0.48779325
## .sig02 -0.37904290 0.25672461
## .sig03 0.03531748 0.06876342
## .sigma 0.49461305 0.53574539
## (Intercept) 1.30810775 1.47151553
## day -0.01277014 0.01663478The “1 + day|id” portion of this equation is requesting that both the intercepts “1” and trajectories “day” are allowed to vary randomly across people “|id”.
This output needs some explaining.
Fixed Effects:
(Intercept): The expected value of stress for the average person on the first time point is 1.39
day: Stress increased marginally over the course of the study days. For every unit increase in day, stress increased by .001 (95% CI = -.01, .02). This is not a significant change (i.e., CI includes zero)
Random Effects:
sd((Intercept)): There is between-person variability in the intercepts of stress (variance = 0.17, sd = 0.42). To know whether this variability is significantly greater than zero, we inspect sig01 from the confidence interval table. We can see that the standardised variance of the intercepts (i.e., the SD) is .42 with a 95% CI from .34 to .49. This does not include zero. So even though the intercept variance in reduced with the addition of time to the empty model, there is still a significant amount of random variance in the intercepts to be explained.
sd(day): There is between-person variability in the within-person trajectories of stress over time (variance = 0.003, sd = 0.05). In other words, although the mean change in stress is negligible, there is some variance around that mean. Some people’s stress increases, some peoples decreases across time. Overall, this means a zero slope in the sample (per fixed effect), but this disguises significant person to person variability.
To know whether this person to person variability in the trajectories of stress is significantly greater than zero, we inspect sig03 from the confidence interval table. We can see that the standardised variance of the slopes (i.e., the SD) is .05 with a 95% CI from .03 to .08. This does not include zero. So even though the fixed effect of time is not-significant, there is still a significant amount of random variance in the slopes to be explained.
- cov((Intercept),days: The correlation between the random intercept and random slope was -0.14, which indicates that those who had higher starting points for stress were more likely to show decreases in stress over time. To know whether this correlation is significantly greater than zero, we inspect sig02 from the confidence interval table. We can see that the relationship between the intercepts and slopes is not significant (95% CI = -.44,.53). This is an interesting coefficient but not focal to our hypotheses so it is okay that it is not significant.
We can plot the within-person stress trajectories to get a sense of the person to person variability:
ggplot(data=stress, aes(x=day, y=stress, group=factor(id), colour="gray"), legend=FALSE) +
geom_smooth(method=lm, se=FALSE, fullrange=FALSE, lty=1, size=.5, color="gray40") +
geom_smooth(aes(group=1), method=lm, se=FALSE, fullrange=FALSE, lty=1, size=2, color="blue") +
xlab("Time") + ylab("Stress") +
theme_classic() +
theme(axis.title=element_text(size=18),
axis.text=element_text(size=14),
plot.title=element_text(size=18, hjust=.5)) +
ggtitle("Within-Person Trajectories of Stress")## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 14 rows containing non-finite values (stat_smooth).## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 14 rows containing non-finite values (stat_smooth).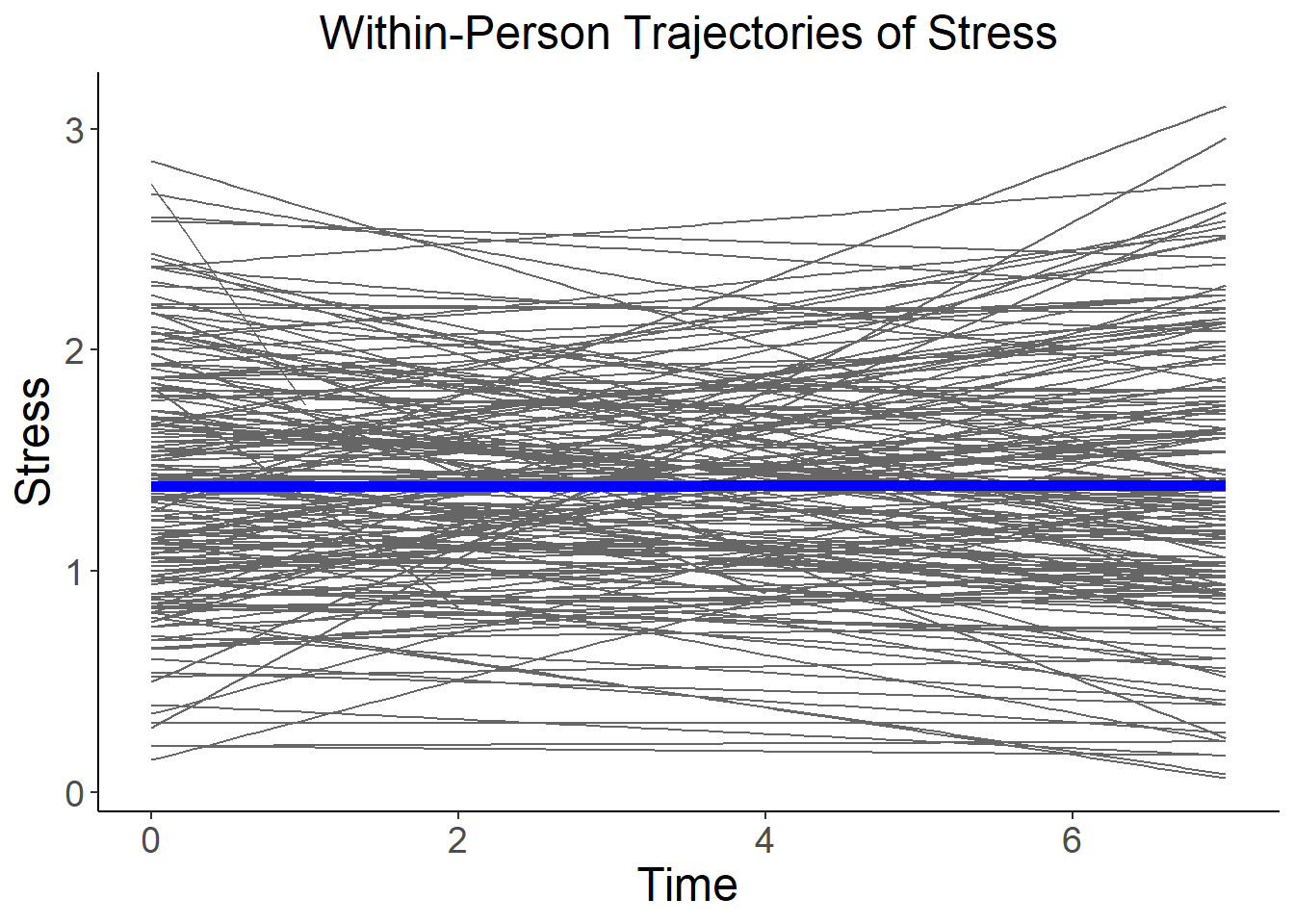
The blue line here shows the fixed intercept (i.e., where the fixed slope crosses zero) and fixed slope of stress on time (i.e., the average trajectory over the sample). As we saw from the MLM output, this line is flat (i.e., no change). However, around this flat fixed effect is significant variability in both the intercepts and slopes. Lets now see if we can explain some of that variability with the addition of our between-person predictor: neuroticism.
Adding a Between-Person Predictor of the Random Intercepts and Slopes
We now add trait neuroticism to the MLM model to see if and how between-person differences in neuroticism are related to the intercepts and trajectories of stress. To examine whether neuroticism explains between-person differences in the intercepts and slopes we must add both the main effect of neuroticism and its interaction with day. The interaction becomes the focal effect: i.e., does the relationship between day and stress depend on neuroticism? In other words, is variability in the trajectories of stress explained by neuroticism?
It is important to grand mean center the neuroticism variable before we fit this model so that the unit of measurement for neuroticism is deviation from the sample mean. To do this, we fit MLM model using the neurotic_gmc variable in the dataset.
time.stress.fit2 <- lmer(formula = stress ~ 1 + day + neurotic_gmc + day*neurotic_gmc + (1 + day|id), data=stress)
summary(time.stress.fit2)## Linear mixed model fit by REML ['lmerMod']
## Formula: stress ~ 1 + day + neurotic_gmc + day * neurotic_gmc + (1 + day |
## id)
## Data: stress
##
## REML criterion at convergence: 2599.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1029 -0.6566 -0.0703 0.5673 4.0427
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## id (Intercept) 0.152930 0.39106
## day 0.002681 0.05178 -0.05
## Residual 0.264449 0.51425
## Number of obs: 1445, groups: id, 190
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 1.386468 0.037591 36.883
## day 0.001229 0.007044 0.175
## neurotic_gmc -0.165306 0.039405 -4.195
## day:neurotic_gmc 0.015582 0.007372 2.114
##
## Correlation of Fixed Effects:
## (Intr) day nrtc_g
## day -0.474
## neurotc_gmc 0.000 0.002
## dy:nrtc_gmc 0.002 -0.019 -0.474confint(time.stress.fit2, method="boot", nsim=100)## Computing bootstrap confidence intervals ...##
## 1 message(s): boundary (singular) fit: see ?isSingular
## 3 warning(s): Model failed to converge with max|grad| = 0.00328609 (tol = 0.002, component 1) (and others)## 2.5 % 97.5 %
## .sig01 0.334151515 0.47418072
## .sig02 -0.352052838 0.41518683
## .sig03 0.030631265 0.06982961
## .sigma 0.490308077 0.53801264
## (Intercept) 1.306518995 1.46858741
## day -0.013403476 0.01237540
## neurotic_gmc -0.238981129 -0.06572291
## day:neurotic_gmc 0.001854072 0.02721801Again, this output will need some explanation:
Fixed Effects:
(Intercept): The expected value of stress for the average person on the first time point is 1.39
day: As before, stress increased marginally over the course of the study days. For every unit increase in day, stress increased by .001 (95% CI = -.01, .02). This is not a significant change (i.e., CI includes zero). But as we saw above, we are not interested in the mean stress change, we are interested here in the variance around that mean trajectory and whether it can be predicted by between-person differences in neuroticism
neurotic_gmc: On average, people with higher neuroticism also tended to experience higher stress (b = 0.17). For every 1 unit increase in neuroticism away from the group mean, there is a corresponding .17 deviation in stress from the group mean. This is a significant relationship (95% CI = .08, .24). Like the mean day fixed effect, this is interesting, but the between-person relation of neuroticism with stress is not the focal effect of interest here.
day:neurotic_gmc: This is the focal coefficient of interest when adding a between person predictor to a MLM model of trajectories. This is because it tells us whether the relationship between time and an outcome (i.e., the change trajectory) differs depending on the level of a between person moderator.
We can see that between-person deviations for the grand mean in neuroticism moderates the relationship between day and stress (b = -.02). The confidence associated with this interaction indicates that it is just significantly greater than zero (95% CI = -.03,-.0001). We can conclude that variance in the trajectories of stress is explained, in part, by between-person differences in neuroticism.
Random Effects:
sd((Intercept)): There is between-person variability in the intercepts of stress (variance = 0.15, sd = 0.39). To know whether this variability is significantly greater than zero, we inspect sig01 from the confidence interval table. We can see that the standardised variance of the intercepts (i.e., the SD) is .39 with a 95% CI from .30 to .47. This does not include zero. So even though the intercept variance is reduced with the addition of neuroticism to the time model, there is still a significant amount of random variance in the intercepts to be explained.
sd(day): There is between-person variability in the within-person trajectories of stress over time (variance = 0.003, sd = 0.05). In other words, although the mean change in stress is negligible, there is some variance around that mean change from person to person. We should note that this variance is slightly decreased with neuroticism in the model.
To know whether this person to person variability in the trajectories of stress is significantly greater than zero, we inspect sig03 from the confidence interval table. We can see that the standardised variance of the slopes (i.e., the SD) is .05 with a 95% CI from .02 to .07. This does not include zero. So even though the interaction of day and neuroticism is significant, there remains a significant amount of random variance in the slopes to be explained beyond neuroticism.
- cov((Intercept),days: The correlation between the random intercept and random slope was -0.03, which indicates that those who had higher starting points for stress were more likely to show decreases in stress over time. To know whether this correlation is significantly greater than zero, we inspect sig02 from the confidence interval table. We can see that the relationship between the intercepts and slopes is not significant (95% CI = -.34,.87).
Plotting the interaction
The moderation of time and neuroticism is significant so we should plot and probe the interaction term, just like we did last year in the moderation analysis session.
We can do this in various ways, but I like the Johnson-Neyman technique we saw last year that plots the conditional slopes across the range of values of a moderator.
Formally, the Johnson-Neyman technique is used to probe significant interactions in order to determine for what values of the moderator the focal predictor is significantly related to the outcome - i.e., to identify the region of significance. This is quickly becoming standard practice in reporting about interactions in multilevel models.
In our case, we are interested to know where in the range of neuroticism the trajectories of stress are and are not significant.
Let’s do that with the johnson_neyman() function from the interactions package using our time.stress.fit2 model object we just fit:
johnson_neyman(model=time.stress.fit2, pred=day, modx=neurotic_gmc)## JOHNSON-NEYMAN INTERVAL
##
## When neurotic_gmc is OUTSIDE the interval [-3.15, 1.79], the slope of day
## is p < .05.
##
## Note: The range of observed values of neurotic_gmc is [-2.02, 1.98]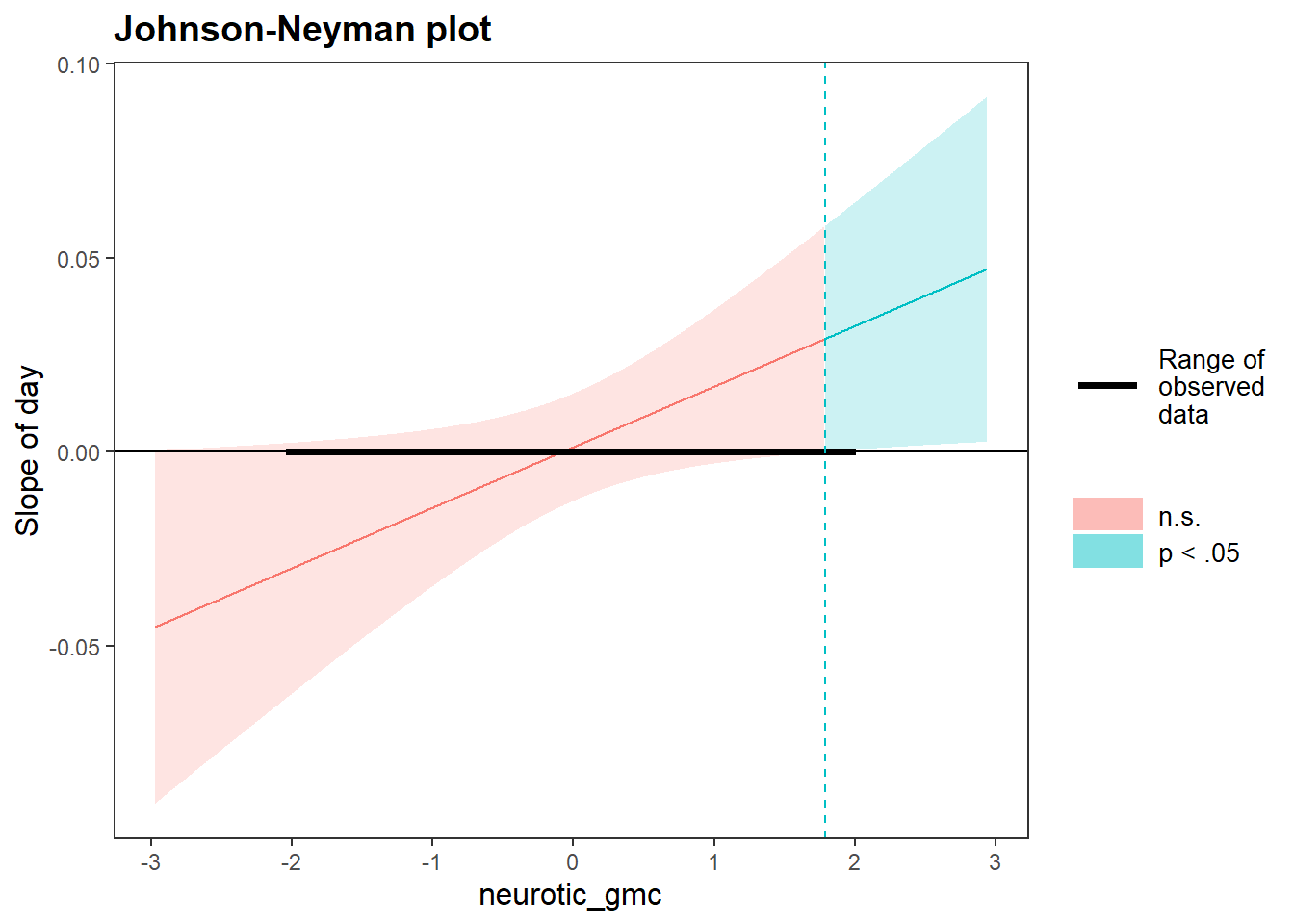
We see from the output and the plot that the within-person trajectories of stress are significant only at high values of neuroticism (i.e., more than 1.79 units from the grand mean), but not at low values of neuroticism (where there is no change in stress across the study period).
Inspection of the sign of the trajectory slopes for day indicates that increases in stress are observed across the study period for those high in neuroticism. This supports our original hypothesis: those people in our sample who are higher in neuroticism had steeper increases in stress over the study period. Awesome (not for them, obviously)!
How its written
The intraclass correlation for stress was first calculated based on the empty model. This was to determine whether the Level 1 outcome (i.e. stress) had substantial between-person variation (Model 1). The intraclass correlation of stress was .40, indicating substantial person to person variance in stress.
In model 2, we added fixed and random effects for the intercepts and time slopes of stress to model 1. Although the fixed effect of time on stress was not different from zero, there was significant between-person variance in both the intercepts and time slopes of stress. As such, intercepts and slopes were permitted to vary randomly in tests of neurotic vulnerability to daily stress.
In model three, we added the cross-level interaction of time (Level 1; within-person) and neuroticism (Level 2; between person) to model two. In this model, time interacted with neuroticism. The positive sign of this interaction is consistent with the interpretation that higher neuroticism is associated with steeper incline trajectory slopes in stress across the period of study.
To illustrate this interaction, we plotted the conditional mean of the trajectory slopes and 95% confidence bands for stress across the range of neuroticism. When neuroticism was below 1.79, the trajectory slopes for stress were non-significant (i.e., confidence bands included zero). However, when neuroticism was above 1.79, the trajectory slopes for stress were positive and significant (i.e., p > .05).
Activity: Testing for Neurotic Vulnerability
Our second research question with the stress data was interested on whether the within-person relationship between stress and negative affect is moderated by neuroticism. That is, whether neurotics have especially large relationships between time varying stress and time varying negative affect. put differently, what we are interested to know here is:
if day-to-day variations in stress (i.e., whether we are higher or lower that our mean on a particular day) correlate with day-to-day variations in negative affect. We should expect that on stressful days when we report higher than our average stress that we would also report higher than our average negative effect. In other words, that these variables have a positive relationship.
However, we also believe that not everybody will have the same stress reactivity. Some will be more stress reactive than others. In other words, some will have larger relationships between stress and negative affect than others.
It is our hypothesis that those with greater within-person stress reactivity are likely to identified by between-person differences in neuroticism. In other words, the relationship between stress and negative affect will be larger in people who score higher on neuroticism and smaller in people who score lower on neuroticism.
In this example, we are predicting daily negative affect. Our level 1 (within-person) predictor is stress and our level 2 (between person) predictor is neuroticism.
Stress Reactivity
We define stress reactivty as the extent to which an individual’s daily negative affect is related to daily stress.
In other words, stress reactivity is the within-person association between daily negative affect and daily stress.
Lets first examine some of our data to see what stress reactivity looks like, just like we did above for the trajectories of stress.
Importantly: because stress is now a predictor in our model, we need to ensure it is centered at the correct level. Here stress is a time varying level one predictor, so we person mean center the stress variable. Doing so means that 0 on the stress variable is the within-person mean stress score, and deviations reflect daily deviation from the mean. Person mean centered stress is the stress_pmc variable in the dataset.
ggplot(data=stress[which(stress$id <= 130),], aes(x=stress_pmc,y=negaff)) +
geom_point() +
stat_smooth(method="lm", fullrange=TRUE) +
xlab("Person Mean Centered Stress") + ylab("Negative Affect") +
facet_wrap( ~ id) +
theme(axis.title=element_text(size=16),
axis.text=element_text(size=14),
strip.text=element_text(size=14))## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 4 rows containing non-finite values (stat_smooth).## Warning in qt((1 - level)/2, df): NaNs produced## Warning: Removed 4 rows containing missing values (geom_point).## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -
## Inf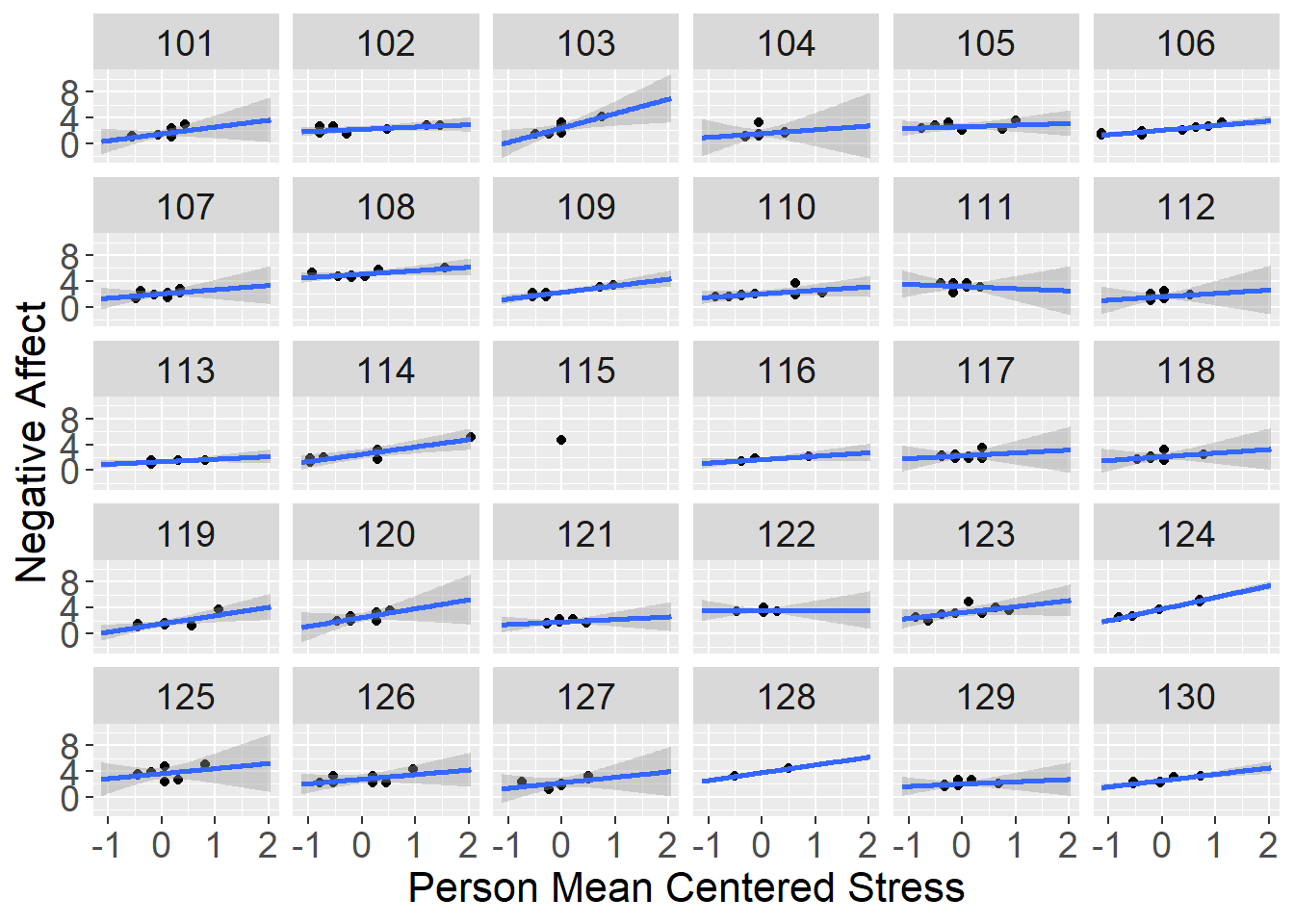
From the panel of plots we get a sense that individuals’ negative affect is higher on days where their stress is higher, but to a different extent for each person. These differences in stress reactivity are indicated by differences in the slope of the regression lines.
The Multilevel Model
Our substantive interest is in describing individual differences in stress reactivity and determining if those differences are related to differences in neuroticism.
The basic Level 1 multilevel model is written as:
negaffti = ai + Bi*(stressti) + eti
where the time-varying outcome variable (varying from day to day), negaffti (negative affect for person i at time point t) is modeled as a function of a within-person intercept, ai (mean stress score for person i); a within-person slope, Bi (the relationship between stress and negative affect for person i); and residual error, eti (the difference between the model predicted negative affect score for person i at time t and the actual negative affect score for person i at time t).
The Level 2 random intercepts (ai) are modeled as:
ai = Ma + Ba(neurotici) + Wai
where the intercept for person i, ai (the negative affect score for person i at mean stress) is modeled as a function of a fixed effect Ma, which describes the mean intercept value across the sample; Ba, which is the relationship of the random negative affect intercepts with neuroticism. The random effect Wai is the residual unexplained intercept variance not explained by neuroticism (the difference between the model predicted negative affect intercept for person i and the actual negative affect intercept for person i).
The Level 2 random slopes (Bi) are modeled as:
Bi = MB + BB(neurotici) + WBi
where the slope for person i, Bi (the relationship betweens tress and negative affect for person i) is modeled as a function of a fixed effect MB, which describes the mean relationship between negative affect and stress across the sample; BB, which is the relationship of the random slope of negative affect on stress with neuroticism. The random effect WBi is the residual unexplained variance in the random slope of negative affect on stress not explained by neuroticism (the difference between the model predicted relationship between stress and negative affect for person i and the actual relationship between stress and negative affect for person i).
Combining Level 1 and Level 2 equations gives us:
negaffti = Ma + (MB + WBi)stressti + Ba(neurotici) + BB(stresstineurotici) + Wai + eti
Note the difference between this model and the stress trajectory model is that we are interested in whether one time varying variable (stress) predicts another time varying variable (negative affect). Not how one time varying variables is changing over time (i.e., the trajectory).
Otherwise, though, the model is the same. We are still interested in the cross-level interaction that tests our focal hypothesis.
Setting up the Empty Model
To start, we fit the empty model that provides us information about how much of the total variance in the outcome variable (negative affect) is within-person variance and how much is between-person variance.
Write the code to fit the empty model for negative affect (negaff):
empty.neg.model <- lmer(formula = negaff ~ 1 + (1|id), data=stress, REML = FALSE)
summary(empty.neg.model)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: negaff ~ 1 + (1 | id)
## Data: stress
##
## AIC BIC logLik deviance df.resid
## 3835.4 3851.2 -1914.7 3829.4 1438
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.8709 -0.6133 -0.1621 0.4657 3.9397
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.4243 0.6514
## Residual 0.6627 0.8141
## Number of obs: 1441, groups: id, 190
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 2.46363 0.05215 47.24Use the intercept add residual variance to calculate the ICC:
.42/(.42+.66)## [1] 0.3888889How much of the variance in negative affect is between-person?
Adding the Time Varying Predictor
OK - let’s add the time varying predictor, stress, which gives us possibility to quantify each individual’s stress reactivity.
Remember to use the person mean centered stress variable here (stress_pmc). Also remeber to call the confidence intervals for the fixed and random effects in this
# Fit and sumarise multilevel model
neg.stress.model <- lmer(formula = negaff ~ 1 + stress_pmc + (1 + stress_pmc|id), data=stress, REML = FALSE)
summary(neg.stress.model)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: negaff ~ 1 + stress_pmc + (1 + stress_pmc | id)
## Data: stress
##
## AIC BIC logLik deviance df.resid
## 3350.1 3381.8 -1669.1 3338.1 1432
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.4593 -0.5945 -0.0916 0.5032 4.5363
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## id (Intercept) 0.4588 0.6773
## stress_pmc 0.1229 0.3506 0.49
## Residual 0.4281 0.6543
## Number of obs: 1438, groups: id, 190
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 2.46773 0.05229 47.19
## stress_pmc 0.76833 0.04590 16.74
##
## Correlation of Fixed Effects:
## (Intr)
## stress_pmc 0.257# Call bootstrap confidence intervals
confint(neg.stress.model, method="boot", nsim=100)## Computing bootstrap confidence intervals ...##
## 2 warning(s): Model failed to converge with max|grad| = 0.00216075 (tol = 0.002, component 1) (and others)## 2.5 % 97.5 %
## .sig01 0.6045142 0.7653287
## .sig02 0.1929561 0.8790943
## .sig03 0.2172461 0.4356629
## .sigma 0.6242001 0.6806855
## (Intercept) 2.3382547 2.6028590
## stress_pmc 0.6788613 0.8524994What is the fixed effect of stress on negative affect (i.e., stress reactivity)?
What is the 95% CI of the stress reactivity fixed effect?
Is there any variability around this fixed effect? (i.e. does stress reactivity vary from person to person?)
Is there any variability in the intercepts of negative affect? (i.e., does mean negative affect vary from person to person?)
Plotting Stress Reactivity
Now lets quickly plot the random stress reactivity across people in our sample:
ggplot(data=stress, aes(x=stress_pmc, y=negaff, group=factor(id), colour="gray"), legend=FALSE) +
geom_smooth(method=lm, se=FALSE, fullrange=FALSE, lty=1, size=.5, color="gray40") +
geom_smooth(aes(group=1), method=lm, se=FALSE, fullrange=FALSE, lty=1, size=2, color="blue") +
xlab("Person Mean Centered Stress") + ylab("Negative Affect") +
theme_classic() +
theme(axis.title=element_text(size=18),
axis.text=element_text(size=14),
plot.title=element_text(size=18, hjust=.5)) +
geom_vline(xintercept=0)+
ggtitle("Within-Person Stress Reactivity")## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 21 rows containing non-finite values (stat_smooth).## `geom_smooth()` using formula 'y ~ x'## Warning: Removed 21 rows containing non-finite values (stat_smooth).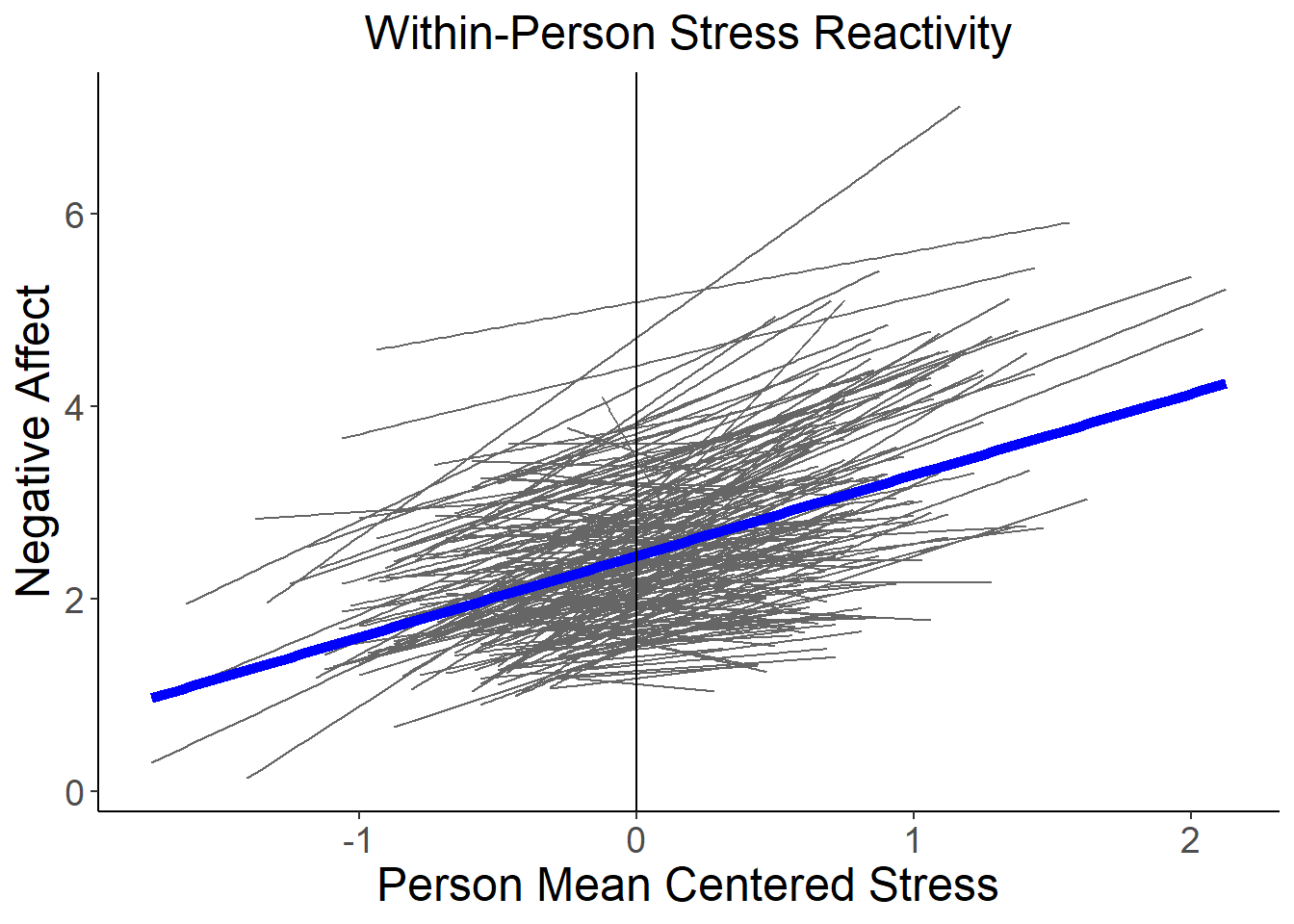
Adding the Level 2 Predictor
We now add trait neuroticism to the model, to see if and how between-person differences in neuroticism are related to stress reactivity. That is, does neuroticism moderate the relationship between stress and negative affect.
Recall in this model we need the stress, neuroticism and the stress by neuroticism interaction in the model. Use the grand mean centered neuroticism variable and the person mean centered stress variable.
# Fit and summarise multilevel model with level 2 predictor and interaction
neg.neurotic.model <- lmer(formula = negaff ~ 1 + stress_pmc + neurotic_gmc + stress_pmc*neurotic_gmc + (1 + stress_pmc|id), data=stress, REML = FALSE)
summary(neg.neurotic.model)## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: negaff ~ 1 + stress_pmc + neurotic_gmc + stress_pmc * neurotic_gmc +
## (1 + stress_pmc | id)
## Data: stress
##
## AIC BIC logLik deviance df.resid
## 3327.6 3369.8 -1655.8 3311.6 1430
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.3464 -0.5871 -0.0780 0.5109 4.5924
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## id (Intercept) 0.3948 0.6284
## stress_pmc 0.1115 0.3339 0.43
## Residual 0.4282 0.6544
## Number of obs: 1438, groups: id, 190
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 2.46793 0.04895 50.414
## stress_pmc 0.77058 0.04520 17.048
## neurotic_gmc -0.26667 0.05132 -5.197
## stress_pmc:neurotic_gmc -0.10689 0.04669 -2.289
##
## Correlation of Fixed Effects:
## (Intr) strss_ nrtc_g
## stress_pmc 0.217
## neurotc_gmc -0.004 -0.002
## strss_pmc:_ -0.002 0.030 0.220# Call bootstrap confidence intervals
confint(neg.neurotic.model, method="boot", nsim=100) ## Computing bootstrap confidence intervals ...## 2.5 % 97.5 %
## .sig01 0.5394335 0.69544658
## .sig02 0.2066989 0.70631922
## .sig03 0.1854029 0.42642656
## .sigma 0.6293607 0.68424139
## (Intercept) 2.3392043 2.55305278
## stress_pmc 0.6881960 0.86482345
## neurotic_gmc -0.3720205 -0.17474490
## stress_pmc:neurotic_gmc -0.2205304 -0.01108505Is the stress*neuroticism interaction significant? (i.e., does a person’s stress reactivity depend on their score of neuroticism)
Plot the Interaction
Let’s plot our interaction using the johnson_neyman() function:
johnson_neyman(model=neg.neurotic.model, pred=stress_pmc, modx=neurotic_gmc)## JOHNSON-NEYMAN INTERVAL
##
## When neurotic_gmc is OUTSIDE the interval [3.81, 50.57], the slope of
## stress_pmc is p < .05.
##
## Note: The range of observed values of neurotic_gmc is [-2.02, 1.98]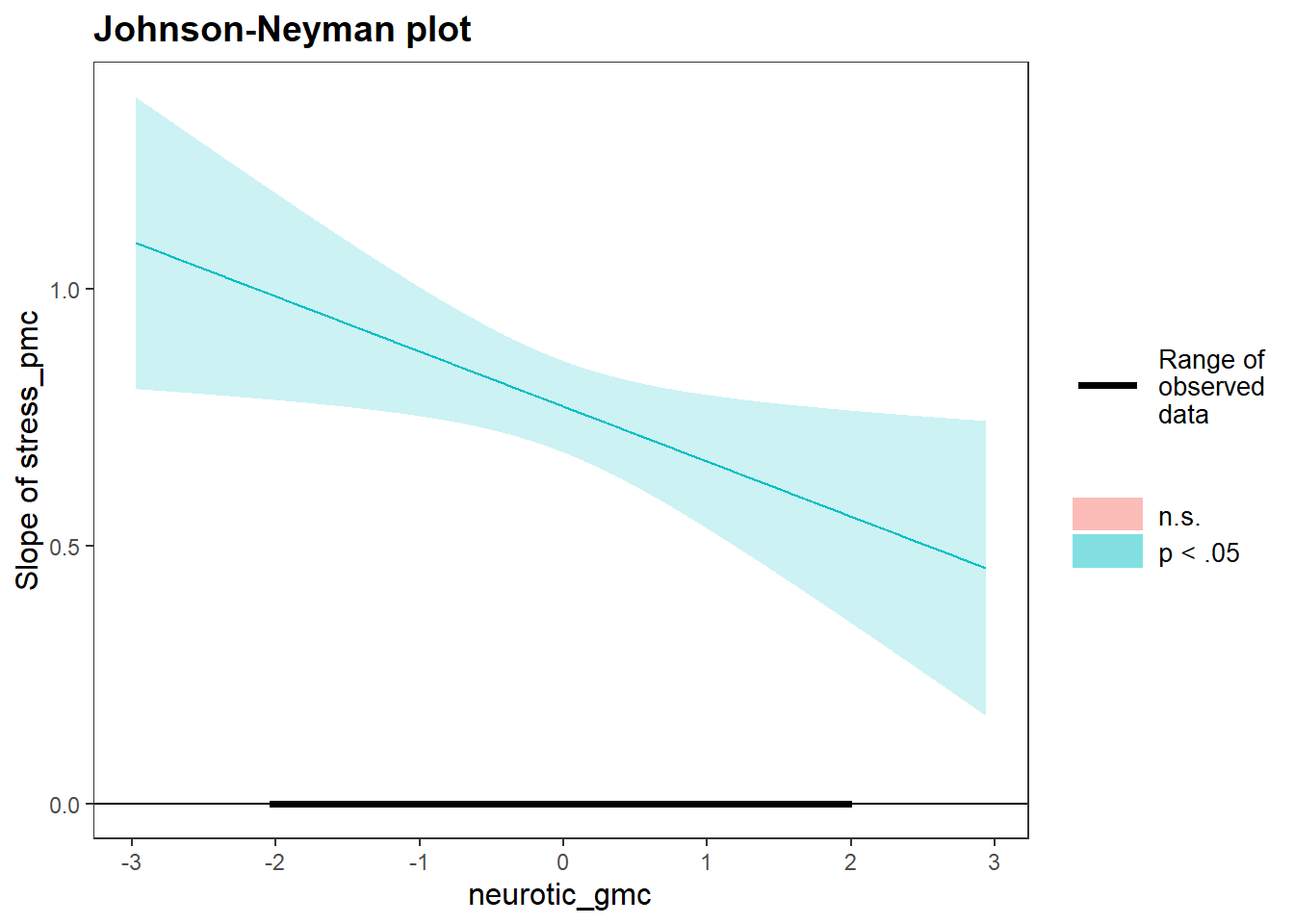
What does this plot tell us?
What is the conclusion with regard to the original research question?