Multiple Regression (LT2)
Now that we know the fundamentals of linear models, we are going to delve a little deeper into regression. We will hone in on the role of prediction in helping us to better understand human behaviour. To do so, we will revisit the straight line equation, but this time focussing on the interpretation of b and β as an expansion from correlation. We look at beta within simple regression – that is regression with only one explanatory variable – and then what happens to the interpretation of beta when we add additional explanatory variables to our linear models. We will finish by looking at model comparisons and how we adjudicate whether the addition of explanatory variables is “worth it” in terms of additional model variance explained.
Learning Outcomes
By the end of this workshop, you should be able to:
Recap a two-parameter linear model to test a simple using simple regression
Extend simple regression to test a three-parameter multiple regression
Plot multiple regression using ggplot()
Complete the lab survey
Load required packages
The required packages are the same as the installed packages. Write the code needed to load the required packages in the below R chunk.
library(supernova)
library(readr)
library(tidyverse)
library(ggplot2)
library(lm.beta)
library(ggpubr)
library(mosaic)
library(Hmisc)
library(car)
library(plyr)The World Happiness Report data
Like in MT10, we are going to use data from the World Happiness Report 2019 (WHR). The World Happiness Report is a landmark survey of the state of global happiness that ranks 156 countries by how happy their citizens perceive themselves to be.
You can go to the WHR site to see what we’ll be working with. Don’t download anything: https://worldhappiness.report/. We will be looking at data from 2019, which includes mean scores for happiness between 2008 and 2018 for each country.
You can access the original .xls file of the data here: https://s3.amazonaws.com/happiness-report/2019/Chapter2OnlineData.xls. Because the file is not very R friendly, I have trimmed it down to include just the variables of interest for this session and saved it as a .csv file. These variables are:
Happiness score or subjective well-being (variable name “Happiness”): The survey measure of happiness is from the January, 2019 release of the Gallup World Poll (GWP) covering years from 2005 to 2018, as well the special GWP surveys for four countries in 2018. Unless stated otherwise, it is the national average response to the question of happiness. The English wording of the question is “Please imagine a ladder, with steps numbered from 0 at the bottom to 10 at the top. The top of the ladder represents the best possible life for you and the bottom of the ladder represents the worst possible life for you. On which step of the ladder would you say you personally feel you stand at this time?” This measure is also referred to as Cantril life ladder, or just life ladder in our analysis.
GDP per capita (variable name “GDP”): The survey measure of GDP is purchasing power parity (PPP) at constant 2011 international dollar prices are from the November 14, 2018 update of the World Development Indicators (WDI). The GDP figures for Taiwan, up to 2014, are from the Penn World Table 9. A few countries are missing the GDP numbers in the WDI release but were present in earlier releases. We use the numbers from the earlier release, after adjusting their levels by a factor of 1.17 to take into account changes in the implied prices when switching from the PPP 2005 prices used in the earlier release to the PPP 2011 prices used in the latest release. The factor of 1.17 is the average ratio derived by dividing the US GDP per capita under the 2011 prices with their counterparts under the 2005 prices.
Gini of household income reported in the GWP (variable name “GINI”): The income inequality variable is described in Gallup’s “WORLDWIDE RESEARCH METHODOLOGY AND CODEBOOK” (Updated July 2015) as “Household Income International Dollars […] To calculate income, respondents are asked to report their household income in local currency. Those respondents who have difficulty answering the question are presented a set of ranges in local currency and are asked which group they fall into. Income variables are created by converting local currency to International Dollars (ID) using purchasing power parity (PPP) ratios.”
Country of data collection (variable name “Country”): The country variable is just the country from which the data were collected.
Year of data collection (variable name “Year”): The year the data were collected.
First, lets load this data into our R environment. Go to the LT2 folder, and then to the workshop folder, and find the “WHR.csv” file. Click on it and then select “import dataset”. In the new window that appears, click “update” and then when the dataframe shows, click import. If you want, you can try running the code below and it might do the same thing (if not put your hand up).
WHR <- read_csv("C:/Users/currant/Dropbox/Work/LSE/PB130/LT2/Workshop/WHR.csv")##
## -- Column specification -------------------------------------------------------------------------------------------------------------------------------------------------------------
## cols(
## Country = col_character(),
## Year = col_double(),
## Happiness = col_double(),
## GDP = col_double(),
## GINI = col_double()
## )WHR## # A tibble: 1,704 x 5
## Country Year Happiness GDP GINI
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Afghanistan 2008 3.72 7.17 NA
## 2 Afghanistan 2009 4.40 7.33 NA
## 3 Afghanistan 2010 4.76 7.39 NA
## 4 Afghanistan 2011 3.83 7.42 NA
## 5 Afghanistan 2012 3.78 7.52 NA
## 6 Afghanistan 2013 3.57 7.52 NA
## 7 Afghanistan 2014 3.13 7.52 NA
## 8 Afghanistan 2015 3.98 7.50 NA
## 9 Afghanistan 2016 4.22 7.50 NA
## 10 Afghanistan 2017 2.66 7.50 NA
## # ... with 1,694 more rowsBefore we begin analysing, recall that we there are missing values in the GDP and gini variables, so they will need to be dealt with. Lets filter the GDP and gini variables to get rid of the cases with missing values.
WHR <- # into existing dataframe
WHR %>% # from existing daraframe
filter(GDP >= "1" & GINI >="0") # Filter GDP at a value of 1 and above and gini at values 0 and above (i.e., rid the dataframe of any non-numeric cases)
WHR## # A tibble: 1,495 x 5
## Country Year Happiness GDP GINI
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Albania 2007 4.63 9.08 0.303
## 2 Albania 2009 5.49 9.16 0.303
## 3 Albania 2010 5.27 9.20 0.303
## 4 Albania 2011 5.87 9.23 0.303
## 5 Albania 2012 5.51 9.25 0.303
## 6 Albania 2013 4.55 9.26 0.303
## 7 Albania 2014 4.81 9.28 0.303
## 8 Albania 2015 4.61 9.30 0.303
## 9 Albania 2016 4.51 9.34 0.303
## 10 Albania 2017 4.64 9.38 0.303
## # ... with 1,485 more rowsOkay, the data are now ready for analyses.
Simple regression
Lets first run a simple regression to refresh our memories about linear modeling with one continuous predictor and one continuous outcome. To recap, simple regression is a two-parameter linear model and we are going to use the happiness and GDP variables in the WHR dataframe to run one. Just like in MT10, our theory here is that as the wealth of a country increases, so self-report happiness also increases. In other words, we are expecting a positive relationship between wealth as measured by GDP and happiness as measured by the Cantril life ladder. Given this expectation, we also expect that we can use a best fitting linear model to make estimations of happiness from GDP.
Before we delve into this topic, lets just clarify the research question and null hypothesis we are testing:
Research Question - Is there a linear relationship between GDP and happiness in the World Happiness Report Data?
Null Hypothesis - The relationship between GDP and happiness will be zero.
Correlation between happiness and GDP
An initial step in any test of relationships is to inspect the extent to which our variables co-vary. That is, their correlation. To do so, we can compute a the correlation coefficient or Pearson’s r. Pearson’s r is a standardized metric and runs between -1 and +1. The closer Pearson’s r is to +/-1, the larger the relationship. The rcorr() function computes Pearson’s r and its associated p value.
rcorr(as.matrix(WHR[,c("GDP","Happiness")], type="pearson"))## GDP Happiness
## GDP 1.00 0.78
## Happiness 0.78 1.00
##
## n= 1495
##
##
## P
## GDP Happiness
## GDP 0
## Happiness 0Pearsons r is .78. According to Cohen (1988, 1992), the effect size is low if the value of r varies around 0.1, medium if r varies around 0.3, and large if r varies more than 0.5. An r of .78 is a very large correlation!
We can visualize this relationship using a scatterplot with ggplot(), whereby data points are plotted for happiness against GDP. We can also draw the best-fitting regression line, which represents the Happiness model, over the same WHR data points
WHR %>%
ggplot(aes(x = GDP, y = Happiness)) + # This is the same as in the visualisation session except we have two variables for the aes() function - GDP and Happiness labeled x for the explanatory variable and y for the outcome
geom_point() + # this is just a reques to plot the points
stat_smooth(method = "lm",
col = "red",
se = FALSE,
size = 1) + # this is a request for the best fitting regression line from the linear model ("lm"), color red and size 1.
theme_classic(base_size = 8) # I prefer the classic theme for scatter plots, but feel free to experiment## `geom_smooth()` using formula 'y ~ x'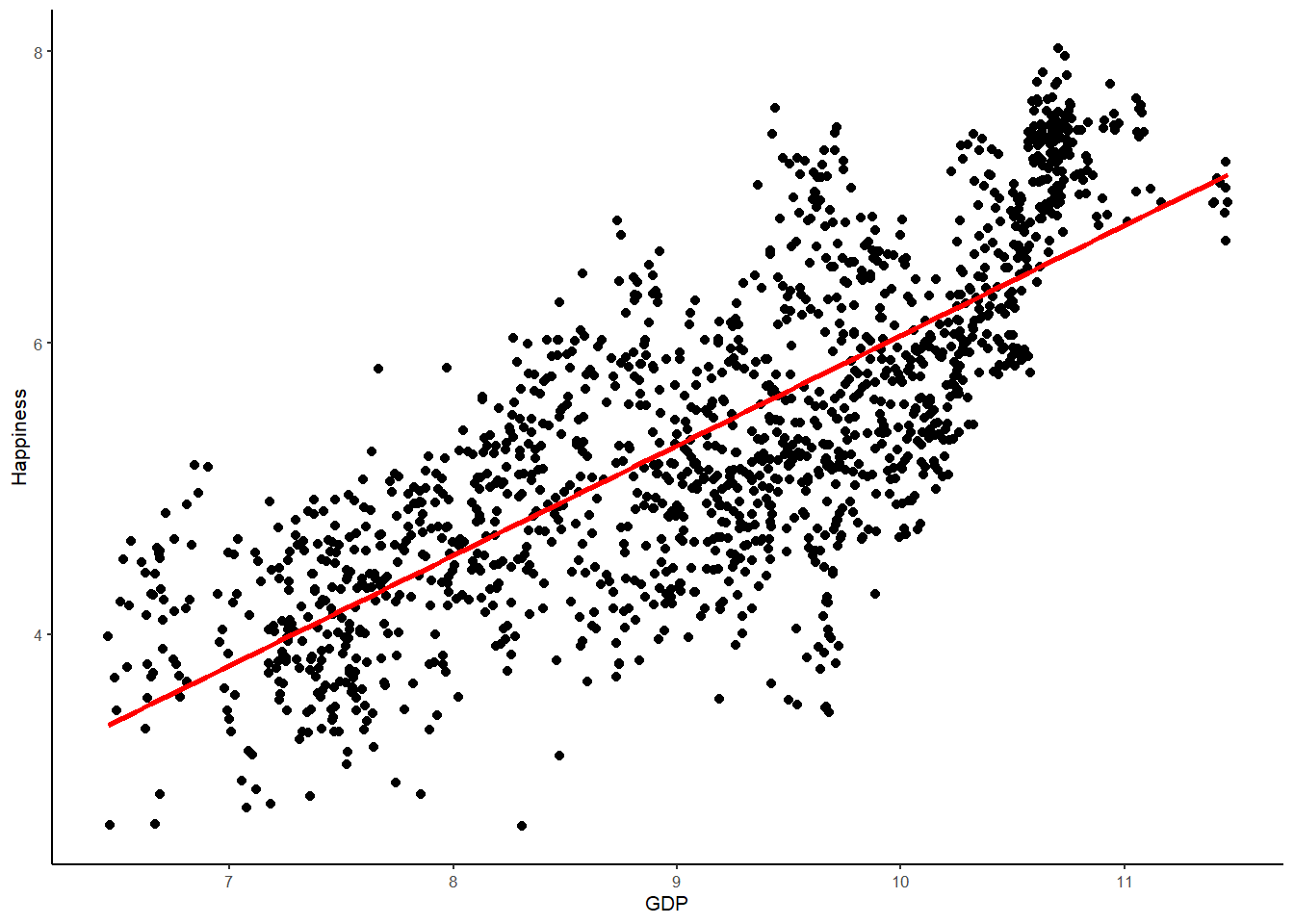
Setting up the simple regression model
Let’s now build the simple regression model in the case where we have a single continuous explanatory variable - in this case GDP. We write the model in notional form like this:
Yi = b0 + b1Xi + ei
Because Xi in the regression model represents the measured GDP of each country, b1 represents the increment that must be added to the predicted happiness of a country for each one-unit increment in GDP. If b1 is the slope of the line, it stands to reason that b0 will be the y-intercept of the line - in other words, the predicted value of happiness when GDP is equal to 0. As the regression line is a straight line, it has to be defined by a slope and an intercept. In the case of a model trying to predict Happiness, of course, the intercept is purely theoretical - it’s impossible for a country to have 0 GDP! But, regardless, it is nevertheless important to know the intercept because it is the anchoring point of the regression line - the point at which the regression line passes through the y-axis.
As with last few weeks, we are going to use the lm() to set up and test the linear model of happiness. The lm() function can detect whether the explanatory variable is continuous (as is the case here), and will by default fit the linear regression model. If the explanatory variable is categorical, lm() will fit a group model. Let’s go ahead and fit the linear regression model for our data and save it in an R object called simple.model.
simple.model <- lm(Happiness ~ 1 + GDP, data = WHR)
summary(simple.model)##
## Call:
## lm(formula = Happiness ~ 1 + GDP, data = WHR)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.34935 -0.50609 0.00075 0.56816 1.98785
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.49770 0.14681 -10.2 <2e-16 ***
## GDP 0.75498 0.01593 47.4 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7126 on 1493 degrees of freedom
## Multiple R-squared: 0.6008, Adjusted R-squared: 0.6005
## F-statistic: 2247 on 1 and 1493 DF, p-value: < 2.2e-16By now the linear model output should be familiar. We have an intercept (b0) of -1.49, which we have established is meaningless because it represents the predicted happiness value when GDP = 0. GDP cannot be 0, so this is simply a hypothetical value used to anchor the regression line.
More interesting is the GDP estimate or b1. Here we have a value of .76. This is interpreted like the slope of a line. Therefore, for every one unit increase in GDP, there is an estimated .76 unit increase in mean happiness. Alongside this slope value we have a standard error (sampling variance) and t ratio. Hopefully we should know how these are interpreted. The p value associated with t is well below .05 and therefore we reject the null hypothesis. GDP is a statistically significant predictor of average happiness!
While we are at it, lets also have R call the standardized estimates by using the lm.beta() function.
lm.beta(simple.model)##
## Call:
## lm(formula = Happiness ~ 1 + GDP, data = WHR)
##
## Standardized Coefficients::
## (Intercept) GDP
## 0.0000000 0.7750845Here you can see that the intercept is zero (the line is drawn through the joint means of happiness and GDP therefore when x = 0, y = 0) and the GDP slope is .78.
Calculating the 95% confidence interval for the coefficients using bootstrapping
As we saw just before Christmas, rather than assume a normal sampling distribution of estimated values when ascertaining the statistical significance of estimates (i.e., the t-distribution), a better approach is to generate a sampling distribution from the available data to arrive at a 95% confidence interval that requires no restrictive assumptions regarding distributions.
Bootstrapping is one method that uses the characteristics of an original sample to produce many thousands of resamples with replacement – estimating coefficients of interest each time. Typically, it is recommended that little benefit is achieved over about 5000 bootstrap resamples, so I recommend you always request 5000 resamples.
In this way, bootsrapping permits us to generate a distribution of estimates that we can rank from low to high and use to cut off the 2.5 and 97.5 percentiles of the distribution (see lecture notes for more details on the mechanics of bootstrapping). Genius!
So lets go ahead and generate a bootstrap sampling distribution of estimates using the Boot() function and save it as a new R object called simple.boot. Note that we are going to request 5000 resamples so that might take a little time to run!
simple.boot <- Boot(simple.model, f=coef, R = 5000) # this function takes the linear model we built earlier and asks for the coeffiencts to be calculated in 5000 resamples with replacement from the original sample (R=5000)## Loading required namespace: bootsummary(simple.boot) # just like the linear model, the summary function outputs the summary of this analysis##
## Number of bootstrap replications R = 5000
## original bootBias bootSE bootMed
## (Intercept) -1.49770 1.0473e-04 0.129140 -1.4992
## GDP 0.75498 -6.1328e-05 0.014241 0.7551What R just did there is take a resample of the original sample and calculate the model coefficients (i.e., b0 and b1) and repeat that process 5000 times! Before the advent of fast computers that would have taken weeks, but R does it in 20 seconds or so.
You can see that the output gives the sample estimates under the original column and then mean estimates from the 5000 resamples in the bootMed column. The difference between the sample and mean bootstrap estimate is given in the bootBias column. Finally, the mean standard error from the 5000 resamples is given in the bootSE column.
We can see that the sample estimates and bootstrap estimates are virtually the same. The bias is tiny.
Now, though, to the important part. With the bootstrap distribution we have just called, we can construct a confidence interval for our estimates. We do this by simply finding the values of b0 (intercept) and b1 (slope) in the bootstrap distribution that reflect the 2.5 and 97.5 percentiles for the upper and lower bounds of the confidence interval.
And, just like normal theory, if zero is not included in the bootstrap 95% confidence interval then we can reject the null hypothesis and conclude that a zero estimate in the population is unlikely.
Lets go ahead and call the bootstrap 95% confidence interval using the confint() function.
confint(simple.boot, level = .95, type = "norm") # this function request the confidence intervals from the simple.boot object. The level is .95 because we want the 95% confidence intervals. The type is norm because we dont want to correct them in any way.## Bootstrap normal confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) -1.7509147 -1.2446961
## GDP 0.7271328 0.7829575Here we see that the range of values for our slope estimate of the relationship between GDP and happiness runs from 0.73 to 0.78 (your values might slightly differ to this, bootstrapping will produce slightly different estimates each time it resamples). Crucially, though, this range does not include zero! We can reject the null hypothesis.
Partitioning variance
As we have been doing every week, lets finally partition the variance in our simple regression model between that explained by the model and that left over(i.e., error). We will use supernova() to do this.
superanova(simple.model)## Registered S3 methods overwritten by 'lme4':
## method from
## cooks.distance.influence.merMod car
## influence.merMod car
## dfbeta.influence.merMod car
## dfbetas.influence.merMod car## Analysis of Variance Table (Type III SS)
## Model: Happiness ~ 1 + GDP
##
## SS df MS F PRE p
## ----- --------------- | -------- ---- -------- -------- ------ -----
## Model (error reduced) | 1140.781 1 1140.781 2246.568 0.6008 .0000
## Error (from model) | 758.128 1493 0.508
## ----- --------------- | -------- ---- -------- -------- ------ -----
## Total (empty model) | 1898.909 1494 1.271The supernova table shows us that the sum of squares for the empty model is 1898.91. This means that adding GDP has minimized the error in the model by 1140.78 sum of squares (i.e., 1898.91 - 758.13 = 1140.78). Indeed, this is alot of error explained by one explanatory variable!
We can also see a PRE or R2 value of .60, which means that GDP explains 60% of the variance in happiness. Similarly there is an F ratio, which is the ratio of the mean square for the model to the mean square for the error left over after subtracting out the model. The larger the ratio of variance explained by the model relative to error, the larger F will be. And, as we saw in the lecture, F is a standardized metric with a smoothed distribution that can be used for Null Hypothesis Significance Testing. We can see that the p value associated with F is zero and therefore we have a statistically significant amount of variance in happiness explained by our regression model. This chimes with what we found when we interpreted the linear model slope.
Multiple regression
As we saw in the lecture, one of the great things about the linear model is that it can take any number of predictor variables and use them to explain one outcome variable. It is often the case in psychology that we would be interested in studying multiple predictor variables, rather than just one. For one thing, the addition of predictor variables allows us to control for other third variable influences on relationships - for example, does x predict y controlling for z? For another thing, the addition of predictor variables allows us to ascertain the relative importance of variables on an outcome - for example, which is the best predictor of y, is it x or is it z? There are other reasons why we would add variables to our linear models - not least to improve the accuracy of our predictions or explain more variance in the outcome. When we add more than one continuous predictor variable to our linear model we are conducting multiple regression.
So lets now employ multiple regression on our WHR dataset and add the Gini coefficient to the simple regression model we just tested. The gini coefficient is a metric of economic inequality and some theories propose that economic inequality can be damaging for happiness. In other words, the greater the gaps between the rich and poor, the less happy people are with their lives. We have just seen that country wealth (i.e., GDP) has a strong positive correlation with happiness but can we improve this model, or explain more variance, by adding Gini to it?
Before we delve into this research question, though, lets just clarify the research question and null hypothesis we are testing:
Research Question - Is there a linear relationship between an optimally weighted combination of GDP and Gini and happiness in the World Happiness Report Data?
Null Hypothesis - The linear relationship between an optimally weighted combination of GDP and Gini and happiness will be zero.
Correlations
The first step in any test of relationships is to inspect the extent to which our variables co-vary. This is especially important for multiple regression because, as we saw in the lecture, the correlations between the predictor variables are removed from the linear model to yield unique effects of the predictor on the outcome (more below). Lets therefore compute the correlation matrix for our variables using the rcorr() function.
rcorr(as.matrix(WHR[,c("GDP","Happiness", "GINI")], type="pearson")) # note how this code is the same as the rcorr code above but include our additional predictor; GINI## GDP Happiness GINI
## GDP 1.00 0.78 -0.32
## Happiness 0.78 1.00 -0.19
## GINI -0.32 -0.19 1.00
##
## n= 1495
##
##
## P
## GDP Happiness GINI
## GDP 0 0
## Happiness 0 0
## GINI 0 0We already know the correlation of GDP and happiness is .78. However, there is some interesting additional information here. The gini coefficient is also correlated with happiness - albeit sharing a much smaller negative relationship of -.19. Likewise, the gini coefficient and GDP are also negatively correlated, with a correlation coefficient of -.32. This correlation is important because it will need to be removed from the linear model so that the regression coefficients of GDP and gini on happiness represent unique effects.
Setting up the linear model
Estimating the parameters of the multiple regression model is accomplished in the exact same way as estimating the parameters of the simple regression model. It all comes down to fitting a line! But in this case, the line is drawn from some optimally weighted combination of predictor variables - GDP and the gini coefficient.
Let’s look at how we build a multiple regression model in the case where we have two continuous explanatory variables - in this case GDP and the gini coefficient. We write the model in notional form like this:
Yi = b0 + b1X1i + b2X2i + ei
Both Yi and ei have the same interpretation in the multiple regression model as in the simple regression model. The outcome variable in both cases is mean happiness of each country, measured as a quantitative variable. And the error term is each country’s deviation from their predicted happiness under the model.
Because X1i and X2i in the regression model represents the measured GDP of each country and the gini coefficient, b1 and b2 represent the increment that must be added to the predicted happiness of a country for each one-unit increment in GDP or the gini coefficient.
If b1 and b2 are the parameters for the slope of the line, it stands to reason that b0 will be the y-intercept of the line - in other words, the predicted value of happiness when GDP and gini are equal to 0. As the regression line is a straight line, it has to be defined by a slope and an intercept. In the case of a model trying to predict Happiness, of course, the intercept is purely theoretical - it’s impossible for a country to have 0 GDP and 0 gini! But, regardless, it is nevertheless important to know the intercept because it is the anchoring point of the regression line - the point at which the regression line passes through the y-axis.
As with all our analyses to date, we are going to use the lm() to build and test the multiple regression model of happiness. The lm() function can detect whether the predictor variables are continuous (as is the case here), and will by default fit the linear regression model. Let’s go ahead and fit the linear regression model for our data and save it in an R object called multiple.model.
multiple.model <- lm(Happiness ~ 1 + GDP + GINI, data = WHR) # notice that all I have done here is add an additional variable to the model. This is a good example of what is happening when we run a multiple regression, we are just adding an additional variable to the existing model.
summary(multiple.model)##
## Call:
## lm(formula = Happiness ~ 1 + GDP + GINI, data = WHR)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.55590 -0.50651 0.01178 0.53932 1.89631
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.98300 0.20210 -9.812 < 2e-16 ***
## GDP 0.77357 0.01674 46.198 < 2e-16 ***
## GINI 0.81773 0.23501 3.480 0.000517 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.71 on 1492 degrees of freedom
## Multiple R-squared: 0.604, Adjusted R-squared: 0.6034
## F-statistic: 1138 on 2 and 1492 DF, p-value: < 2.2e-16By now, hopefully the linear model output should be familiar. We have an intercpet(b0) of -1.98, which we have established is meaningless because it represents the predicted happiness value when GDP = 0 and gini = 0. GDP cannot be 0, so this is simply a hypothetical value used to anchor the regression line.
More interesting are the slope estimates. First is the GDP slope estimate or b1. Here we have a value of .77. Holding gini constant, for every one unit increase in GDP, there is an estimated .77 unit increase in mean happiness. Notice this is different from the GDP estimate in the simple model (.73). This is not a mistake. Regression coeffcients in multiple regression are calculated differently than in simple regression becuase the shared variance, or correlation, of the predictor variables is removed from the model. In other words, the regression coefficients in multiple regression show the predictive ability of each predictor on the outcome over and above the variance shared between the predictors.
The second coefficient of interest is the slope coefficient for gini or b2. Here we have a value of .81. Holding GDP constant, for every one unit increase in gini, there is an estimated .81 unit increase in mean happiness. Notice here that we have a slight anomoly. The correlation between gini and happiness is -.19, but when we control for GDP the relationship becomes positive. This means that, if you remove the variablity in inequality (gini) that is accounted for by country wealth (GDP), the remaining variability shares a postive correlation with happiness.
Alongside this slope values we have a standard error (sampling variance) and t ratio. Hopefully we should know how these are interpreted. The p value associated with t is well below .05 for both slope estimates and therefore we reject the null hypothesis. GDP and gini are statistically significant predictors of average happiness!
With the intercept and regression coeffcients, we can use our model to make predictions about Happiness. We write our model in notational form like this:
Yi = -1.98 + 0.77X1i + 0.82X2i
If we were to use this formula to caluate each persons model implied Happiness score, we would end up with a set of predicted estimates. To do this, we can use the predict() function to calcuate the predicted scores and save them in a new variable called predicted (much like we have been doing in previous weeks)
WHR$predicted <- predict(multiple.model)
WHR## # A tibble: 1,495 x 6
## Country Year Happiness GDP GINI predicted
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Albania 2007 4.63 9.08 0.303 5.29
## 2 Albania 2009 5.49 9.16 0.303 5.35
## 3 Albania 2010 5.27 9.20 0.303 5.38
## 4 Albania 2011 5.87 9.23 0.303 5.41
## 5 Albania 2012 5.51 9.25 0.303 5.42
## 6 Albania 2013 4.55 9.26 0.303 5.43
## 7 Albania 2014 4.81 9.28 0.303 5.44
## 8 Albania 2015 4.61 9.30 0.303 5.46
## 9 Albania 2016 4.51 9.34 0.303 5.49
## 10 Albania 2017 4.64 9.38 0.303 5.52
## # ... with 1,485 more rowsInstead of different predicted scores being returned on the basis of scores one predictor (as we saw when we did a simple regression), you will see that the predicted scores returned by the regression model now depend on country scores for both GDP and gini. Pretty neat!
Error or the residuals are calculated in the same way as in the other linear models we have tested. That is, the difference between the model predicted happiness score and the observed happiness score. We can use the resid() function to calculate the residuals and save these as a new variable called residuals in the dataframe
WHR$residuals <- resid(multiple.model)
WHR## # A tibble: 1,495 x 7
## Country Year Happiness GDP GINI predicted residuals
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Albania 2007 4.63 9.08 0.303 5.29 -0.653
## 2 Albania 2009 5.49 9.16 0.303 5.35 0.133
## 3 Albania 2010 5.27 9.20 0.303 5.38 -0.115
## 4 Albania 2011 5.87 9.23 0.303 5.41 0.462
## 5 Albania 2012 5.51 9.25 0.303 5.42 0.0922
## 6 Albania 2013 4.55 9.26 0.303 5.43 -0.876
## 7 Albania 2014 4.81 9.28 0.303 5.44 -0.629
## 8 Albania 2015 4.61 9.30 0.303 5.46 -0.855
## 9 Albania 2016 4.51 9.34 0.303 5.49 -0.977
## 10 Albania 2017 4.64 9.38 0.303 5.52 -0.879
## # ... with 1,485 more rowsIn multiple regression, whats awesome about the predicted values is that they not only give us a means of calculating the error left over in the model (i.e., residuals), but they also give us a means of plotting the line that best fits our multiple regression model. That is, the one that reflects the relationship between the outcome and the optimally weighted combination of predictor variables. To visualize this, lets create 2 plots - one that shows the simple relationship between happiness and GDP and one that shows the multiple relationship between happiness and a combination of GDP and gini. In both plots, we will demarcate the empty model (i.e., the mean of happiness) with a blue line.
# plot 1, simple regression model
WHR %>%
ggplot(aes(x = GDP, y = Happiness)) +
geom_point() +
geom_hline(aes(yintercept=mean(Happiness)), col="blue", size=1) +
stat_smooth(method = "lm",
col = "red",
se = FALSE,
size = 1) +
ggtitle("Simple Regression Model") +
stat_cor() + # the retruns the correlation coefficient
stat_regline_equation(label.y = 7) + # this returns the GLM equation
theme_classic(base_size = 8)## `geom_smooth()` using formula 'y ~ x'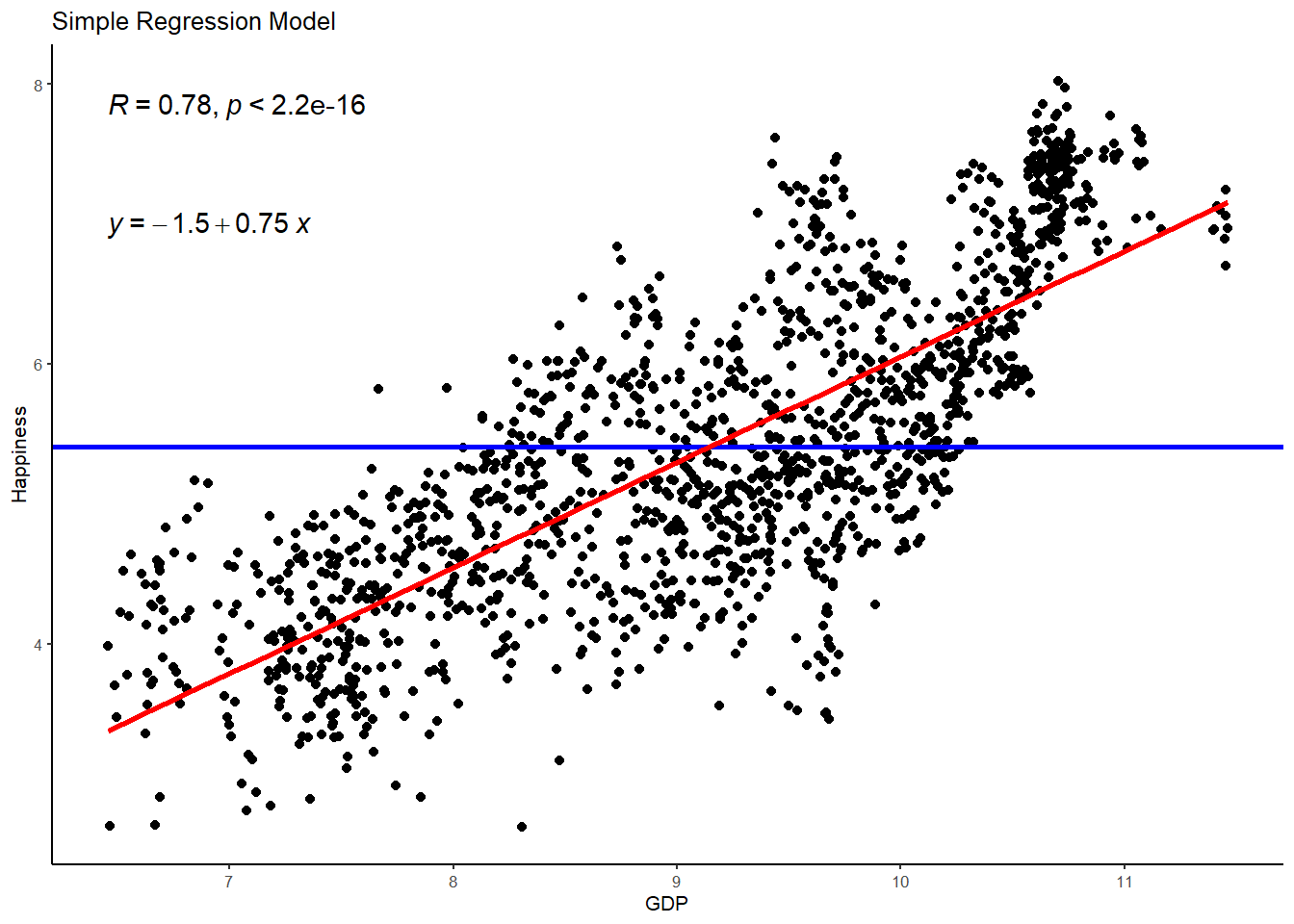
# plot 2, multiple regression model
WHR %>%
ggplot(aes(x = predicted, y = Happiness)) +
geom_point() +
geom_hline(aes(yintercept=mean(Happiness)), col="blue", size=1) +
stat_smooth(method = "lm",
col = "red",
se = FALSE,
size = 1) +
ggtitle("Multiple Regression Model") +
stat_cor() + # the retruns the correlation coefficient
stat_regline_equation(label.y = 7) + # this returns the GLM equation
theme_classic(base_size = 8)## `geom_smooth()` using formula 'y ~ x'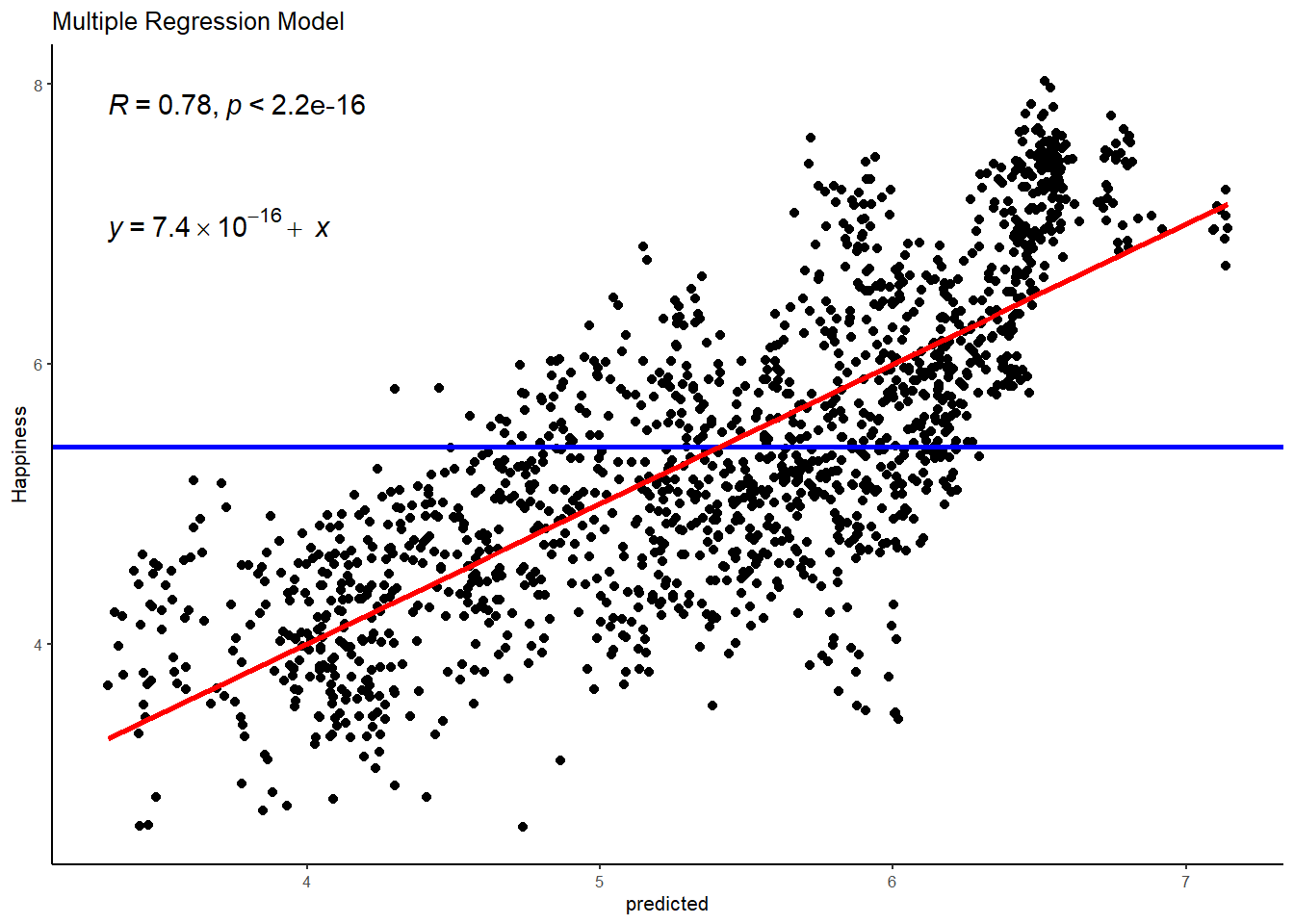
You can see here that the addition of gini - though a statistically significant predictor - hasn’t really done a great deal in terms of explaining additional empty variance in happiness. The model R is the same and the regression line largely unchanged.
Finally, lets also have R call the standardized estimates by using the lm.beta() function. Standardized estimates are really important in multiple regression because they allow us to directly compare estimates.
lm.beta(multiple.model)##
## Call:
## lm(formula = Happiness ~ 1 + GDP + GINI, data = WHR)
##
## Standardized Coefficients::
## (Intercept) GDP GINI
## 0.00000000 0.79416946 0.05981558You will see above that the unstandardized estimate for GINI looks very different to the standardized estimate for GINI. Every 1 unit increase in GINI equates to a .82 increase in happiness according to our model. On the surface, that looks like a much larger effect than GDP (.77) but we know from the correlation coefficient that the relationship is in fact much smaller. So what is going on here? Well, the relationship appears bigger in the linear model because GINI has a very different scale of measurement than GDP (0-1 versus 0-12). So a 1 unit increase in GINI has a very different meaning to a 1 unit increase in GDP. This is why standardized estimates are so useful when comparing coefficients - they force the unit of measurement to the same scale so that effects can be directly compared. Here we can see that although gini appears to have a relationship with happiness, the standardised estimates tell us that that relationship is very small (B = .06). Still statistically significant, but much smaller than we would infer from the unstandardised estimates.
Calculating the 95% confidence interval for the coefficients using bootstrapping
By now, we know that the sampling distribution (i.e., t-ratio) is not the most optimal way to conduct null hypothesis testing. As we have seen, bootstrapping is the most satisfactory method that provides a confidence interval for the estimates without making restrictive assumptions regarding the distribution of variables and estimates. So lets go ahead and generate a bootstrap sampling distribution of estimates using the Boot() function and save it as a new R object called multiple.boot. Note that we are going to request 5000 resamples so that might take a little time to run!
multiple.boot <- Boot(multiple.model, f=coef, R = 5000)
summary(multiple.boot) ##
## Number of bootstrap replications R = 5000
## original bootBias bootSE bootMed
## (Intercept) -1.98300 -0.0027080 0.224941 -1.98525
## GDP 0.77357 0.0002274 0.016426 0.77382
## GINI 0.81773 0.0009130 0.300321 0.82664We can see that the sample estimates and bootstrap estimates are virtually the same. The bias is tiny.
Lets go ahead and call the bootstrap 95% confidence interval using the confint() function.
confint(multiple.boot, level = .95, type = "norm") ## Bootstrap normal confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) -2.4211729 -1.5394185
## GDP 0.7411525 0.8055403
## GINI 0.2281932 1.4054318Here we see that the range of values for our slope estimate of the relationship between GDP and happiness runs from 0.74 to 0.81. Likewise, the range of values for our slope estimate of the relationship between gini and happiness runs from 0.22 to 1.41 (your values might slightly differ to this, bootstrapping will produce slightly different estimates each time it resamples). Crucially, these ranges do not include zero! We can therefore reject the null hypotheses.
Partitioning variance
As we did with the simple regression model, lets partition the variance in our simple regression model between that explained by the model and that left over (i.e., error). We will use supernova() to do this.
superanova(multiple.model)## Analysis of Variance Table (Type III SS)
## Model: Happiness ~ 1 + GDP + GINI
##
## SS df MS F PRE p
## ----- --------------- | -------- ---- -------- -------- ------ -----
## Model (error reduced) | 1146.884 2 573.442 1137.694 0.6040 .0000
## GDP | 1075.729 1 1075.729 2134.220 0.5886 .0000
## GINI | 6.102 1 6.102 12.107 0.0080 .0005
## Error (from model) | 752.026 1492 0.504
## ----- --------------- | -------- ---- -------- -------- ------ -----
## Total (empty model) | 1898.909 1494 1.271Like in the simple regression, the supernova table shows us that the sum of squares for the empty model is 1898.91. This should not be surprising because the empty model is exactly the same whether we test for simple or multiple regression - that is, the mean of happiness as the baseline model. So adding gini has minimized the error further in the model by 6.102 sum of squares. Is this alot? Certainly does not look like it. Furthermore, the PRE or R2 is exactly the same as the simple model - .60 or 60% of the variance explained. So was the addition of gini worth it? There are a couple of ways we can test this.
First is the F ratio, which is the ratio of the mean square for the model to the mean square for the error left over after subtracting out the model. The crucial advantage of this metric of fit over R2 is that it accounts for the degrees of freedom in the model. With 1 additional predictor in the model we now have 2 degrees of freedom and an F ratio of 1137.69. This is statistically significant, but lower than the F ratio for the simple regression model (2246). It seems adding gini to our model is quite expensive in terms of model fit relative to the empty model.
As we saw in the lecture, though, there is another more direct test of whether adding gini was worth it. Rather than inspect the F ratio for the model comparison to the empty model, we can also calculate F for the comparison between the simple model (GDP only) and the full model (GDP and gini). The calculation for doing this F test is:
F = ((R2full - R2simple)/(dffull-dfsimple))/((1-R2full)/dffull) - see lecture notes for formula
Lets quickly run that calculation with our numbers from the supernova output
((.6040-.6008)/(2-1))/((1-.6040)/1492)## [1] 12.05657We have a F ratio of 12.06. F is a standardized metric with a smoothed distribution that can be used for Null Hypothesis Significance Testing. In order to know whether an F of 12.06 is large enough to be considered statistically significant we need to inspect a table of F distributions and find the critical value of F with 1,1492 degrees of freedom that cuts off 95% of the distribution. F tables are freely available online, but here is one for you:

We can see that with 1 degree of freedom in the numerator and over 120 degrees of freedom in the denominator, we would need a F ratio larger than 3.84 to consider the addition of gini statistically meaningful. Our F ratio is larger than this and therefore we prefer the full model - there is an improvement of fit with gini added but I would caution that it is small and significant only because of the very large sample size (making even small increases in R2 significant)
So what do we conclude in relation to our research question? Well a combination of GDP and gini explain a statistically significant amount of variance in Happiness. Controlling for each other, both gini and GDP have positive relationships with Happiness, but GDP is by far the most meaningful predictor.
Exercise
Okay, lets now give you a chance to set up and test a multiple regression. For this, lets use a dataset that contain data on employee goals and levels of enthusiasms in the workplace. This is a real dataset collected in the field from a sample of accountants working at an accountancy firm in Bristol, UK. In this dataset are responses to a survey assessing employees’ levels of two motivational goals for work and their enthusiasm - all responded to on Likert scales running between 1 and 5.
The first goal measured is a task goal, which is employees’ tendency to strive to develop their skills and abilities, advance their learning, understand material, or complete or master a task (e.g., “I work to master tasks and overcome challenges”). The second is an ego goal, which measures employee tendencies to prove one’s competence and to gain favorable judgments about it from others (e.g., “I work to receive bonuses and awards”). Enthusiasm was measured using an items referring to how much enjoyment and excitement one felt at work (e.g., “I feel a sense of excitement when I’m working”)
Because task goals are more controllable and focus on personal growth rather than normative performance, it was hypothesised that task goals would contribute more to enthusiasm at work than would ego goals. To test this hypothesis, we are going to run a multiple regression to see how different goals predict enthusiasm.
Before we delve into this topic, lets just clarify the research question and null hypothesis we are testing:
Research Question - Is there a linear relationship between a combination of task and ego goals and enthusiasm in accountants
Null Hypothesis - The relationship between task and ego goals and enthusiasm will be zero.
Before we start, lets load the goals dataframe to the R environment. Go to the LT2 folder, and then to the workshop folder, and find the “goals.csv” file. Click on it aand then select “import dataset”. In the new window that appears, click “update” and then when the dataframe shows, click import. If you want, you can try running the code below and it might do the same thing (if not put your hand up).
goals <- read_csv("C:/Users/currant/Dropbox/Work/LSE/PB130/LT2/Workshop/goals.csv")## Warning: Missing column names filled in: 'X1' [1]##
## -- Column specification -------------------------------------------------------------------------------------------------------------------------------------------------------------
## cols(
## X1 = col_double(),
## Particpant = col_double(),
## Task = col_double(),
## Ego = col_double(),
## Enthusiasm = col_double()
## )goals## # A tibble: 257 x 5
## X1 Particpant Task Ego Enthusiasm
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 35 4.71 2.5 5
## 2 2 201 2.86 2.83 5
## 3 3 97 3.5 2 2.25
## 4 4 27 4.86 1.33 4
## 5 5 149 3.57 1 4.75
## 6 6 227 4 1 3.5
## 7 7 31 3.14 1.17 2.5
## 8 8 218 3.29 2.33 3.25
## 9 9 204 3 1.67 3
## 10 10 113 3.29 1 4.75
## # ... with 247 more rowsTask 1 - Calcualte the correlation coefficient for the relationships between goals and enthusiasm
Now use the rcorr() function to call the correlation coefficient - or Pearson’s r - for the relationship between GINI and happiness.
rcorr(as.matrix(goals[,c("Task", "Ego", "Enthusiasm")], type="pearson"))## Task Ego Enthusiasm
## Task 1.00 0.33 0.5
## Ego 0.33 1.00 0.2
## Enthusiasm 0.50 0.20 1.0
##
## n= 257
##
##
## P
## Task Ego Enthusiasm
## Task 0.0000 0.0000
## Ego 0.0000 0.0015
## Enthusiasm 0.0000 0.0015# fill in the ?? gap here for the explanatory variable and the correlation type (pearson)What is the correlation between Task and Enthusiasm?
Is this a small, medium, or large correlation?
Is this correlation statistically significant?
What is the correlation between Ego and Enthusiasm?
Is this a small, medium, or large correlation?
Is this correlation statistically significant?
Task 2 - Setting up the linear model
Now lets set our up our linear multiple regression model to examine the coefficient estimates. Remember that Enthusiasm is our outcome variable and Task and Ego are our predictors. Don’t forget to save the linear model in a new R object. I suggest goals.model
goals.model <- lm(Enthusiasm ~ 1 + Task + Ego, data=goals) # add ?? variables to the linear model code
summary(goals.model) # add the new R object to the summary function##
## Call:
## lm(formula = Enthusiasm ~ 1 + Task + Ego, data = goals)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.85772 -0.29429 0.04294 0.36295 1.20759
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.34847 0.21023 11.171 < 2e-16 ***
## Task 0.48902 0.05811 8.416 2.87e-15 ***
## Ego 0.02384 0.03844 0.620 0.536
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5024 on 254 degrees of freedom
## Multiple R-squared: 0.2483, Adjusted R-squared: 0.2424
## F-statistic: 41.96 on 2 and 254 DF, p-value: < 2.2e-16What is the intercept?
What is the slope for Task?
What is the interpretation of the Task slope?
What is the t-ratio?
What is the p value (remember that e-values mean zero)?
Do we accept or reject the null hypothesis?
What is the slope for Ego?
What is the interpretation of the Ego slope?
What is the t-ratio?
What is the p value (remember that e-values mean zero)?
Do we accept or reject the null hypothesis?
Task 3 - The standardized estimates
In the below chunk, use the lm.beta() function to calcuate the standardized estimate for the slopes of taks and ego.
lm.beta(goals.model) # add goals.model to the lm.beta function##
## Call:
## lm(formula = Enthusiasm ~ 1 + Task + Ego, data = goals)
##
## Standardized Coefficients::
## (Intercept) Task Ego
## 0.00000000 0.48533210 0.03576563What is the standardised slope for task?
What is the standardised slope for ego?
Which is the best predictor of Enthusiasm?
Task 4 - Bootstrap 95% confidence interval for the model estimates
Lets go ahead generate a bootstrap sampling distribution of the estimates and use it to call the bootstrap 95% confidence interval using the confint() function.
goals.boot <- Boot(goals.model, f=coef, R = 5000)
summary(goals.boot) ## add the goals.model and stipulate how many resamples you want to run (typically 5,000)##
## Number of bootstrap replications R = 5000
## original bootBias bootSE bootMed
## (Intercept) 2.348466 -0.0080738 0.237577 2.338381
## Task 0.489021 0.0031519 0.065905 0.491579
## Ego 0.023841 -0.0016945 0.036725 0.021872confint(goals.boot, level = .95, type = "norm") # add the bootstrap model you just created to this code## Bootstrap normal confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) 1.89089645 2.82218244
## Task 0.35669766 0.61504095
## Ego -0.04644518 0.09751532What is the bootstrap 95% confidence interval for the slope of task on ethusiasm?
Do we accept or reject the null hypothesis?
What is the bootstrap 95% confidence interval for the slope of ego on ethusiasm?
Do we accept or reject the null hypothesis?
Task 5 - Paritioning variance
We’ve established whether there is a statistically significant relationship between or variables and set up the linear model. Lastly, how much variance in enthusiasm explained by a combination of task and ego? We can answer this question using the supernova() function in R, which breaks down the variance in enthusiasm due to the model (ie., task and ego) and error (i.e., variance left over once we’ve subtracted out the model).
supernova(goals.model) # add goals.model to the supernova function## Analysis of Variance Table (Type III SS)
## Model: Enthusiasm ~ 1 + Task + Ego
##
## SS df MS F PRE p
## ----- --------------- | ------ --- ------ ------ ------ -----
## Model (error reduced) | 21.182 2 10.591 41.961 0.2483 .0000
## Task | 17.877 1 17.877 70.829 0.2180 .0000
## Ego | 0.097 1 0.097 0.385 0.0015 .5357
## Error (from model) | 64.108 254 0.252
## ----- --------------- | ------ --- ------ ------ ------ -----
## Total (empty model) | 85.290 256 0.333What is the total variance or sum of squares for enthusiasm?
How is that sum of squares partitioned between the model?
And the Error?
What is the percentage of variance explained by the model?
What is the F ratio?
What is the p value?
What do we conclude in relation to our research question?