Polynomials and Common Corrections (LT10)
To this point in the course, we have analysed data under the assumption that it is behaving nicely. That is, it comes from cross-sectional and/or experimental sources and that relationships are linear. However, what if we have data collected over several months or years, which is common in developmental psychology? Or what if relationships follow a shape that is not linear, such as curved or u-shaped, which is common in the behavioural sciences? This week we will take an initial look into some of these common complications (among others) and begin to explore how we deal with them.
Learning outcomes
At the end of today’s workshop you should be able to do the following:
Conduct a polynomial regression
Correct a correlation for range restriction
Correct a correlation for unreliability
Load required packages
The required packages are the same as the installed packages. Write the code needed to load the required packages in the below R chunk..
library(mosaic)
library(car)
library(Hmisc)
library(psych)
library(tidyverse)
library(ggplot2)Polynomial regression
Polynomial regression is used to test the shape of non-linear relationships. Those that are assumed to have a shape that is different to a straight line.
Lets say, for example, that we are interested in the the happiness of British college students over the last 10 years. We have reason to suspect that the data will be non-linear. Although college student happiness seems to rise after the recession, there is good evidence that this rise slowed down in recent years due to several macro-economic factors including increased competition and availability of graduate jobs.
Okay, given this information, we need to create a polynomial regression that can approximate the levels of happiness of British college students across the past 10 years. I’m going to do something different in terms of data entry this week. I’m going to show you how to create your own data frames. First I’m going to enter the year variable covering 2010 to 2020.
Year <- c(2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020) # create an object year that contains (c) 2010 through 2020Then I’m going to create the happiness variable, which contains mean happiness data from students in the UK who completed the NSS survey. Happiness is captured on a 1 to 7 scale, with 1 indicating not at all happy to 7 extremely happy.
Happiness <- c(4.835, 4.970, 5.085, 5.160, 5.310, 5.260, 5.235, 5.255, 5.235, 5.210, 5.175)Finally, I am going to combine the Year and Happiness variables into a new data frame called happiness.
happiness <- data.frame(Year, Happiness)
happiness## Year Happiness
## 1 2010 4.835
## 2 2011 4.970
## 3 2012 5.085
## 4 2013 5.160
## 5 2014 5.310
## 6 2015 5.260
## 7 2016 5.235
## 8 2017 5.255
## 9 2018 5.235
## 10 2019 5.210
## 11 2020 5.175As you can see, we now have a data object in R called happiness that houses the data of interest.
Okay, so we have the data. Whenever you are conducting polynomial regression, it is important to first mean center the predictor so that there is a neighborhood of zero (i.e., the mean value is 0 and thus there are an equal number of points above and below 0 - remember that the mean is the balancing point of the distribution!). Note we are not changing anything about the distribution of the predictor variable, just the units so that the shape of the trend can be plotted through 0. In our case, finding the mean of the predictor is easy, it is just the middle year - in this case 2015. So we just subtract the observed year from 2015 to center it.
happiness$Year <- (happiness$Year-2015)
happiness## Year Happiness
## 1 -5 4.835
## 2 -4 4.970
## 3 -3 5.085
## 4 -2 5.160
## 5 -1 5.310
## 6 0 5.260
## 7 1 5.235
## 8 2 5.255
## 9 3 5.235
## 10 4 5.210
## 11 5 5.175Now let’s plot these values to get an idea of the shape of the trend. We can do this really easily in ggplot give visualization methods we have covered way back in the Michaelmas term.
plot <- ggplot(happiness, aes(x = Year, y = Happiness)) + geom_point() + theme_classic()
plot
Okay, so we can see here that the trend is definitely not linear. Just as we suspected, there is an initial period of growth in happiness following the recession, but this slows down from around 2014 (-1 on our recoded year variable).
Yet it is not sufficient to just visualize this trend, we need to statistically ascertain its best fitting shape. For this we will run polynomial regression.
The 1st degree linear model
As we saw in the lecture, polynomial regression just uses the linear model, but adds powers to the predictor variable to model the shape of a relationship.
You might be asking; at what degree of the polynomial stop? Well, it depends on the degree of precision that we seek. The greater the degree of the polynomial, the greater the accuracy of the model, but the greater the difficulty in calculating; remember that we must also verify the significance of coefficients that are found.
I am minded at this point to remind students of Occam’s razor - the principal of parsimony. Named after William of Occam who believed that ‘it is vain to do with more what can be done with less’. Science should be no different. An elegant equation is more likely to be right than an ugly one that seems to fit the data. In other words, natural symmetry and honed brevity are more likely to fit the data in the end.
As such, it is unlikely that psychologists would go further than the 3rd degree when testing polynomial regression. We will also stop here.
First then, we need to test the linear model to ascertain the fit of a straight line to the data. We know it will not fit optimally because we have plotted the points, but it nevertheless gives us a baseline model with which to compare the addition of polynomial terms. So let’s go ahead and run the linear model and save it as a new R object called ‘fit1’.
fit1 <- lm(Happiness ~ 1 + Year, data = happiness)
summary(fit1)##
## Call:
## lm(formula = Happiness ~ 1 + Year, data = happiness)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.17568 -0.06727 0.01568 0.05489 0.18205
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.15727 0.03306 155.988 <2e-16 ***
## Year 0.02932 0.01046 2.804 0.0206 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1097 on 9 degrees of freedom
## Multiple R-squared: 0.4663, Adjusted R-squared: 0.407
## F-statistic: 7.863 on 1 and 9 DF, p-value: 0.02057We can see that the linear model fits the data reasonably well. There is 47% variance in happiness explained by year. And the slope coefficient for year is positive and statistically significant (i.e., p < .05). Lets just bootstrap those estimates as all good statisticians should.
fit1.boot <- Boot(fit1, f=coef, R = 5000) ## Loading required namespace: bootsummary(fit1.boot)##
## Number of bootstrap replications R = 5000
## original bootBias bootSE bootMed
## (Intercept) 5.157273 0.00937710 0.035748 5.164922
## Year 0.029318 -0.00023009 0.013775 0.029708confint(fit1.boot, level = .95, type = "norm") ## Bootstrap normal confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) 5.077830500 5.21796075
## Year 0.002549483 0.05654706And bootstrapping supports the conclusions of normal theory testing.
But the question is, can we do better? Can we explain more variance by adding powers of the predictor to model the potential for non-linear effects? For this we need to add the polynomial terms.
The second degree polynomial model (quadratic shape)
The first polynomial we are going to add is the 2nd degree polynomial term, which models a quadratic shape - that is, whether the effect accelerates or decelerates over time. For this we will add a third parameter to the simple regression model, which is year^2 (or year to the second power). Lets go ahead and do that now and save the model as a new R object called ‘fit2’.
fit2 <- lm(Happiness ~ 1 + Year + I(Year^2), data = happiness) # must specify the polynomial term in I() to tell R this is polynomial (and not Year specified twice)
summary(fit2)##
## Call:
## lm(formula = Happiness ~ 1 + Year + I(Year^2), data = happiness)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.046888 -0.018834 -0.003159 0.002040 0.086748
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.263159 0.017655 298.110 < 2e-16 ***
## Year 0.029318 0.003696 7.933 4.64e-05 ***
## I(Year^2) -0.010589 0.001323 -8.002 4.36e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.03876 on 8 degrees of freedom
## Multiple R-squared: 0.9407, Adjusted R-squared: 0.9259
## F-statistic: 63.48 on 2 and 8 DF, p-value: 1.235e-05Okay, now we are getting somewhere! We can see that both the linear and quadratic effects are significant. The negative sign of the quadratic slope indicates that while the linear trend is positive, it decelerates over time.
We can also see that the addition of the 2nd degree polynomial has substantially increased the variance explained in the model - from 47% to 94%!
Like always, lets just check this with bootstrapping.
fit2.boot <- Boot(fit2, f=coef, R = 5000)
summary(fit2.boot)##
## Number of bootstrap replications R = 5000
## original bootBias bootSE bootMed
## (Intercept) 5.263159 0.00094376 0.0218218 5.263576
## Year 0.029318 -0.00226898 0.0064324 0.028575
## I(Year^2) -0.010589 -0.00013418 0.0021800 -0.010611confint(fit2.boot, level = .95, type = "norm")## Bootstrap normal confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) 5.21944472 5.304984777
## Year 0.01897980 0.044194520
## I(Year^2) -0.01472705 -0.006181742And the bootstrapping support the normal theory testing.
As we saw in LT2, it is not an especially good idea to compare models directly using R2 because R2 does not take into consideration the degrees of freedom in the model.
There is another more direct test of whether adding our 2nd degree polynomial significantly improves the model. Rather than inspect the R2 the models, we can also calculate F for the comparison between the simple model (linear effect only) and the full model (linear and quadratic). The calculation for doing this F test is:
F = ((R2full - R2imple)/(dffull-dfsimple))/((1-R2full)/dffull) - see lecture notes for formula
But we can also request it directly in R using anova(). Lets do that now for models fit1 and fit2.
anova(fit1, fit2)## Analysis of Variance Table
##
## Model 1: Happiness ~ 1 + Year
## Model 2: Happiness ~ 1 + Year + I(Year^2)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 9 0.10822
## 2 8 0.01202 1 0.096197 64.026 4.361e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1This output shows us that the addition of the quadratic term to the linear model has reduced the residual (error) sum of squares by .10 (.11 - .01). In the context of the 1 degree of freedom spent adding the quadratic term to the linear model (i.e., 1), the F ratio associated with this reduction in error is large and significant (64.03, p < .05). There is an improvement of fit with the quadratic term added!
The 3rd degree polynomial model (cubic shape)
Finally, we can check to see whether the fit is improved further with the addition of a polynomial term to the third power. To do so, we just add a fourth parameter; Year^3 to our model. Lets do that now and save it as a new R object called ‘fit3’.
fit3 <- lm(Happiness ~ 1 + Year + I(Year^2) + I(Year^3), data = happiness)
summary(fit3)##
## Call:
## lm(formula = Happiness ~ 1 + Year + I(Year^2) + I(Year^3), data = happiness)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.032774 -0.014802 -0.001253 0.003199 0.072634
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.2631585 0.0150667 349.324 4.16e-16 ***
## Year 0.0143638 0.0081282 1.767 0.1205
## I(Year^2) -0.0105886 0.0011293 -9.376 3.27e-05 ***
## I(Year^3) 0.0008401 0.0004209 1.996 0.0861 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.03308 on 7 degrees of freedom
## Multiple R-squared: 0.9622, Adjusted R-squared: 0.946
## F-statistic: 59.44 on 3 and 7 DF, p-value: 2.403e-05In this model, the slopes for the linear and cubic effects are not significant, and it therefore appears that the best model is the polynomial of 2nd degree. We can confirm this using bootstrapping.
fit3.boot <- Boot(fit3, f=coef, R = 5000)
summary(fit3.boot)##
## Number of bootstrap replications R = 5000
## original bootBias bootSE bootMed
## (Intercept) 5.26315851 0.0032172 0.0222110 5.26585411
## Year 0.01436383 -0.0017667 0.0130556 0.01485362
## I(Year^2) -0.01058858 -0.0006097 0.0043215 -0.01078275
## I(Year^3) 0.00084013 0.0001413 0.0010518 0.00081634confint(fit3.boot, level = .95, type = "norm")## Bootstrap normal confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) 5.216408543 5.303473989
## Year -0.009458036 0.041719071
## I(Year^2) -0.018448851 -0.001508902
## I(Year^3) -0.001362640 0.002760306And the bootstrapping results support the normal theory.
Furthermore, look at the Multiple R-squared: in the 2nd degree model it is 94.07%, while in the 3rd degree model it is 96.22%. Yes there has been an increase in accuracy of the model, but we know that adding any variable will increase R2 due if nothing else but to chance. Therefore, let’s compare the cubic model with the quadratic model using anova() to see if the addition of the cubic term was worth it.
anova(fit2, fit3)## Analysis of Variance Table
##
## Model 1: Happiness ~ 1 + Year + I(Year^2)
## Model 2: Happiness ~ 1 + Year + I(Year^2) + I(Year^3)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 8 0.0120198
## 2 7 0.0076595 1 0.0043603 3.9848 0.0861 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Since the p-value is greater than 0.05, we accept the null hypothesis: there wasn’t a significant improvement of the model. The quadratic model with the 2nd degree polynomial is the best fit.
Plotting the polynomial
Great, we have identified the shape of the trend - it is quadratic with a deceleration!
The last thing to do now is to represent graphically the result. In fact, ggplot has an excellent layer called stat_smooth that plots polynomials for whatever degree you have found to fit the data best. In our case we have found a 2nd degree polynomial to fit the data best, so we just add this layer (+) to our initial plot of the data points above (i.e., plot).
plot + stat_smooth(method = "lm", formula = y ~ x + I(x^2), size = 1) # the smooth method just uses the linear model to plot the shape of the relationship using I(x^2), which is what we found to fit the data best.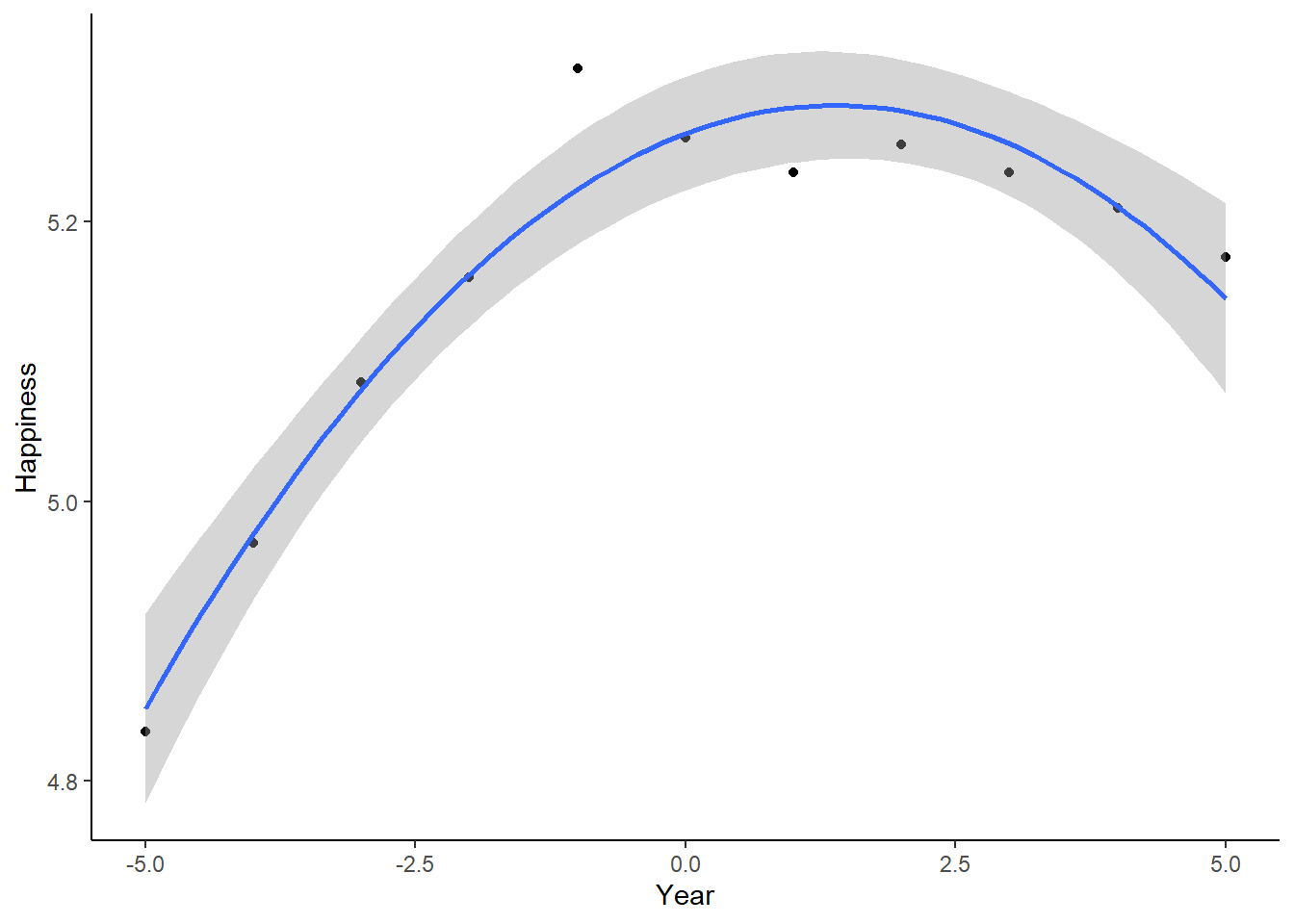
And there you have it! You have just successfully conducted your first polynomial regression. Not that difficult, right?!
Correcting for range restriction
Another topic we covered in the lecture was correcting correlations for two common artefacts that can influence their estimation; range restriction and unreliability.
Let’s start with range restriction and look how we correct correlations that come from restricted ranges. In this example, we are going to use some of my perfectionism data retrieved from college students.. Rather than look at the relationship of time or country on perfectionism scores, we are going to look at age.
Our research question is: is there a relationship between age and perfectionism in American adults?
First, lets load this data into our R environment. Go to the LT10 folder, and then to the workshop folder, and find the “perfectionism.csv” file. Click on it and then select “import dataset”. In the new window that appears, click “update” and then when the dataframe shows, click import. If you want, you can try running the code below and it might do the same thing (if not put your hand up).
perfectionism <- read_csv("C:/Users/CURRANT/Dropbox/Work/LSE/PB130/LT10/Workshop/perfectionism.csv")##
## -- Column specification --------------------------------------------------------
## cols(
## id = col_double(),
## year = col_double(),
## spp = col_double(),
## age = col_double()
## )Because college student data has a restricted range of age (i.e., between 18 and 25), we need to correct the correlation observed in college students to yield a likely correlation in the population as a whole. To see this, lets just run the favstats function on the age variable.
favstats(~age, data=perfectionism)## min Q1 median Q3 max mean sd n missing
## 18 19.46 20.3 21.8 25.96 20.71161 1.719917 159 0The range of values is small going from 18 to 25.96, with a mean of 20.17 and SD of 1.72. This is a classic scenario for range restriction correction - when the predictor variable is restricted at one end of the distribution (in this case the lower end).
So let’s first calculate the correlation coefficient for age and perfectionism (variable name; spp) in the restricted sample.
rcorr(as.matrix(perfectionism[,c("spp","age")], type="pearson"))## spp age
## spp 1.00 -0.18
## age -0.18 1.00
##
## n= 159
##
##
## P
## spp age
## spp 0.0254
## age 0.0254As we can see, in our restricted data there is a small negative correlation between age and perfectionism. The correlation is -0.18, and the p value is 0.03. But we know the correlation is restricted, so lets estimate it in the adult population using the range restriction correction we covered in the lecture.
Doing the range restriction calculation
A correction for range restriction that is well known is Thorndike Case 2:
Let R be the unrestricted correlation, r the restricted correlation, S the unrestricted standard deviation, s the restricted standard deviation, then
R = (rS / s) / sqrt(1 - r^2 + r^2 * (S^2 / s^2)).
Estimating the population SD
For this formula to hold, we need the population standard deviation (S). We could find the population range of ages and work a SD for the American adult population. But lets for the sake of this task assume that we do not have access to the population SD. I am assuming this because it is often the case that we do not know the SD in the population and thus we need to somehow estimate it.
To estimate the population SD from the distributional properties of a restricted sample, Cohen (1959) proposed the ratio: SD^2/(X - Xc)^2. In other words, the sample variance (SD) over the squared difference between the sample mean (X) and point of truncation (Xc).
This ratio is useful because a normal distribution, truncated at Xc, will have a unique value of SD^2/(X - Xc)^2. Two normal functions, the standard deviation in standardized form in a restricted distribution, and the z-score representing the truncation point, are tabled directly against Cohen’s ratio (see below table). These tabled values can then easily be used to correct means, standard deviations, and correlations.
Cohen’s Ratio, Restricted SD, and z Score for Truncation Point
The sample of interest is assumed to be a random sample from a normal population truncated at some unknown point. Cohen’s ratio is calculated from the sample mean and standard deviation (X, SD) and the lowest or highest observed variate-value (Xc) depending on where the sample is restricted. In this example, truncation is assumed to occur at the upper end of the distribution (i.e., we are missing older age groups). If truncation has occurred at the lower end of a distribution, the method described is the same except that Xc is taken as the lowest observed sample value. Let’s calculate Cohen’s ratio with the available information:
Cohen’s ratio: SD^2/(X - Xc)^2
1.72^2/(20.71161 - 25.96)^2## [1] 0.1074001Once Cohen’s ratio has been calculated, the closest tabled value (Table 1) is located. The corresponding z-cut, that is, the z-score identifying the point of truncation, and the standard deviation in a normal distribution truncated at that point may then be obtained from Table 1. Here we can see that a Cohen’s ratio of 0.11 corresponds with a truncated SD of .992 and a z score of -2.95. Since the standard deviation in Table 1 is the standardized value of the standard deviation after truncation, that tabled value also represents the proportional reduction in the standard deviation due to range restriction. The observed sample standard deviation may be corrected by:
population SD = restricted SD / truncated SD
1.72/0.992## [1] 1.733871And there we have it - the estimated SD in the population! Incidentally, we can also estimate the corrected mean using this information. All we have to do is take the truncated value - in this case the highest score 25.96 and subtract out the z-score multiplied by the restricted SD.
25.96 - (-2.95*1.72)## [1] 31.034When we do so we get an unrestricted mean age of 31. Still a slight underestimation based on what we know about the mean US population (approx 38 years), but nevertheless closer than what our original sample assumes.
Correcting the correlation
Now we have an estimated population SD of 2.36, lets now correct our correlation of -0.08 for range restriction. To do so, we can use the psych package, which implements Thorndike’s case 2 using the rangeCorrection() function.
rangeCorrection(-0.18,1.733871,1.72,case=2) # this function takes the correlation, followed by the population SD, followed by the sample SD, and then stipualtes case 2 for Thorndike's case 2 correction## [1] -0.181404And here we can see that the corrected correlation is more or less the same as the uncorrected correlation. This is likely because the estimated population SD was quite close to the sample SD. If we increase the population SD a little to 4 you can see that the corrected correlation difference also increases.
rangeCorrection(-0.10,4,1.72,case=2)## [1] -0.2275957This is what happens when we correct our correlations for range restriction - the bigger the difference in the variance of the population and sample, the larger the difference between the uncorrected and corrected correlation.
Correcting for unreliability
The second correction often applied to correlations is that for unreliability. As we saw in the lecture and in LT8, unreliability is when a measure contains error. Now, all measures contain some error, but some contain more than others. We can estimate how much error is contained in a measure by calculating the ratio of true score variance to overall variance in a variable.
To illustrate this, I want to return to the data we collected on personality in LT8 and correct the correlation between neuroticism and openness for unreliability.
First, lets load this data into our R environment. Go to the LT10 folder, and then to the workshop folder, and find the “bigfive.csv” file. Click on it and then select “import dataset”. In the new window that appears, click “update” and then when the dataframe shows, click import. If you want, you can try running the code below and it might do the same thing (if not put your hand up).
bigfive <- read_csv("C:/Users/CURRANT/Dropbox/Work/LSE/PB130/LT10/Workshop/bigfive.csv")##
## -- Column specification --------------------------------------------------------
## cols(
## .default = col_double(),
## `Event Index` = col_character(),
## `UTC Date` = col_character(),
## `Local Date` = col_character(),
## `Tree Node Key` = col_character(),
## `Repeat Key` = col_logical(),
## `Participant Public ID` = col_character(),
## `Participant Starting Group` = col_logical(),
## `Participant Status` = col_character(),
## `Participant Completion Code` = col_logical(),
## `Participant External Session ID` = col_logical(),
## `Participant Device Type` = col_character(),
## `Participant Device` = col_character(),
## `Participant OS` = col_character(),
## `Participant Browser` = col_character(),
## `Participant Monitor Size` = col_character(),
## `Participant Viewport Size` = col_character(),
## Checkpoint = col_logical(),
## `Task Name` = col_character()
## )
## i Use `spec()` for the full column specifications.Before we work on this, we need to run some preliminaries to clean it up. Let’s do that now.
# first filter out NAs
bigfive <-
bigfive %>%
filter(e1 >= "1")
# note I specify car:: here becuase car and tidyverse have a recode function and I want R to use the car recode function
bigfive$a1 <- car::recode(bigfive$a1r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$c2 <- car::recode(bigfive$c2r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$e2 <- car::recode(bigfive$e2r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$n2 <- car::recode(bigfive$n2r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$a3 <- car::recode(bigfive$a3r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$c4 <- car::recode(bigfive$c4r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$e5 <- car::recode(bigfive$e5r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$c5 <- car::recode(bigfive$c5r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$n5 <- car::recode(bigfive$n5r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$a6 <- car::recode(bigfive$a6r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$e7 <- car::recode(bigfive$e7r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$n7 <- car::recode(bigfive$n7r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$o7 <- car::recode(bigfive$o7r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$a8 <- car::recode(bigfive$a8r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$o9 <- car::recode(bigfive$o9r, "1=5; 2=4; 3=3; 4=2; 5=1")
bigfive$c9 <- car::recode(bigfive$c9r, "1=5; 2=4; 3=3; 4=2; 5=1")
# select out the items
bigfive <- select(bigfive, e1, e2, e3, e4, e5, e6, e7, e8, c1, c2, c3, c4, c5, c6, c7, c8, c9, o1, o2, o3, o4, o5, o6, o7, o8, o9, o10, a1, a2, a3, a4, a5, a6, a7, a8, a9, n1, n2, n3, n4, n5, n6, n7, n8)
# calculate variables
bigfive <- bigfive %>%
mutate(neuroticism = (n1 + n2 + n3 + n4 + n5 + n6 + n7 + n8)/8)
bigfive <- bigfive %>%
mutate(openness = (o1 + o2 + o3 + o4 + o5 + o6 + o7 + o8 + o9 + o10)/10)Okay, great we have the data in good shape. Just like for range restriction, lets first calculate the uncorrected correlation between neuroticism and openness.
rcorr(as.matrix(bigfive[,c("neuroticism","openness")], type="pearson"))## neuroticism openness
## neuroticism 1.00 0.43
## openness 0.43 1.00
##
## n= 14
##
##
## P
## neuroticism openness
## neuroticism 0.124
## openness 0.124We can see that the uncorrected correlation is 0.43, but not significant (p< .05). But don’t worry about that, we have a small sample of only 14. Lets focus on the correlation estimate and how much it has been attenuated by measurement unreliability.
Calculating reliability
The first step in correcting the correlation for unreliability is to calculate the reliability of the variable. If you recall, neuroticism has 8 items and openness has 10, we first collate these items and then calculate Cronbach’s alpha. We did this by hand in the lecture, and by using the alpha() function from the psych package in the workshop. So lets go ahead and do that now.
neuroticism <- select(bigfive, n1, n2, n3, n4, n5, n6, n7, n8)
openness <- select(bigfive, o1, o2, o3, o4, o5, o6, o7, o8, o9, o10)
psych::alpha(neuroticism)##
## Reliability analysis
## Call: psych::alpha(x = neuroticism)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.83 0.83 0.93 0.37 4.8 0.064 2.9 0.71 0.41
##
## lower alpha upper 95% confidence boundaries
## 0.7 0.83 0.95
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## n1 0.82 0.82 0.89 0.40 4.6 0.068 0.078 0.48
## n2 0.81 0.81 0.88 0.38 4.4 0.068 0.087 0.48
## n3 0.80 0.80 0.91 0.36 3.9 0.076 0.083 0.39
## n4 0.76 0.76 0.84 0.31 3.2 0.093 0.068 0.34
## n5 0.79 0.79 0.91 0.34 3.7 0.083 0.092 0.34
## n6 0.87 0.87 0.94 0.49 6.7 0.051 0.041 0.54
## n7 0.81 0.80 0.91 0.37 4.1 0.073 0.088 0.43
## n8 0.79 0.79 0.87 0.35 3.7 0.078 0.065 0.36
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## n1 14 0.57 0.59 0.58 0.449 2.1 0.92
## n2 14 0.64 0.63 0.64 0.516 2.8 1.05
## n3 14 0.74 0.74 0.71 0.645 3.1 0.95
## n4 14 0.91 0.92 0.95 0.860 3.4 1.22
## n5 14 0.82 0.80 0.75 0.702 2.9 1.41
## n6 14 0.24 0.23 0.11 0.068 2.6 1.02
## n7 14 0.68 0.69 0.65 0.572 3.1 0.92
## n8 14 0.78 0.79 0.80 0.706 3.1 0.86
##
## Non missing response frequency for each item
## 1 2 3 4 5 miss
## n1 0.29 0.43 0.21 0.07 0.00 0
## n2 0.00 0.57 0.14 0.21 0.07 0
## n3 0.00 0.29 0.36 0.29 0.07 0
## n4 0.00 0.36 0.07 0.36 0.21 0
## n5 0.29 0.00 0.43 0.14 0.14 0
## n6 0.07 0.50 0.29 0.07 0.07 0
## n7 0.00 0.29 0.43 0.21 0.07 0
## n8 0.00 0.21 0.50 0.21 0.07 0psych::alpha(openness)## Warning in psych::alpha(openness): Some items were negatively correlated with the total scale and probably
## should be reversed.
## To do this, run the function again with the 'check.keys=TRUE' option## Some items ( o6 o9 o10 ) were negatively correlated with the total scale and
## probably should be reversed.
## To do this, run the function again with the 'check.keys=TRUE' option##
## Reliability analysis
## Call: psych::alpha(x = openness)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.55 0.62 0.9 0.14 1.7 0.18 3.6 0.46 0.12
##
## lower alpha upper 95% confidence boundaries
## 0.2 0.55 0.9
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## o1 0.46 0.53 0.88 0.113 1.14 0.21 0.14 0.095
## o2 0.57 0.65 0.89 0.172 1.87 0.17 0.15 0.164
## o3 0.45 0.53 0.88 0.110 1.11 0.22 0.14 0.095
## o4 0.41 0.53 0.85 0.109 1.11 0.23 0.15 0.095
## o5 0.38 0.48 0.83 0.095 0.94 0.25 0.14 0.087
## o6 0.66 0.72 0.91 0.224 2.59 0.14 0.12 0.229
## o7 0.60 0.64 0.87 0.165 1.78 0.16 0.13 0.115
## o8 0.41 0.46 0.83 0.087 0.86 0.23 0.13 0.071
## o9 0.61 0.67 0.89 0.182 2.01 0.16 0.15 0.229
## o10 0.56 0.64 0.90 0.164 1.77 0.16 0.16 0.185
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## o1 14 0.637 0.70 0.68 0.506 3.6 0.85
## o2 14 0.149 0.25 0.21 -0.013 4.4 0.74
## o3 14 0.661 0.72 0.70 0.502 4.0 1.04
## o4 14 0.753 0.72 0.73 0.629 3.6 1.01
## o5 14 0.820 0.84 0.85 0.728 3.2 0.97
## o6 14 -0.027 -0.14 -0.21 -0.261 3.8 1.12
## o7 14 0.202 0.30 0.29 -0.032 3.1 1.07
## o8 14 0.846 0.89 0.92 0.790 4.1 0.73
## o9 14 0.237 0.17 0.14 -0.026 2.9 1.21
## o10 14 0.437 0.31 0.23 0.147 3.4 1.40
##
## Non missing response frequency for each item
## 1 2 3 4 5 miss
## o1 0.00 0.07 0.43 0.36 0.14 0
## o2 0.00 0.00 0.14 0.36 0.50 0
## o3 0.00 0.07 0.29 0.21 0.43 0
## o4 0.00 0.07 0.50 0.14 0.29 0
## o5 0.00 0.29 0.29 0.36 0.07 0
## o6 0.00 0.14 0.29 0.21 0.36 0
## o7 0.07 0.21 0.36 0.29 0.07 0
## o8 0.00 0.00 0.21 0.50 0.29 0
## o9 0.07 0.36 0.29 0.14 0.14 0
## o10 0.14 0.14 0.07 0.43 0.21 0The first and most important output tells us that the neuroticism variable has a Cronbach alpha of .83 and the openness variable a Cronbach alpha of .55.
Correcting the correlation
With this information we can do a simple correction to the correlation between these variables, which accounts for the measurement error or unreliability inherent to the two variables. Recall from the lecture that the calculation for correcting the correlation for measurement error is:
rxy / sqrt(rxx * ryy),
where rxy is the uncorrected correlation, rxx is the Cronbach alpha for x and ryy the Cronbach alpha for y.
Plugging these numbers into R..
.43 / sqrt(.83*.55)## [1] 0.6364262We find that the correct correlation is .64. That’s quite an increase! This is because the openness variable has poor reliability and therefore the measure contains a lot of error that is irrelevant to neuroticism. Lets see what happens if openness contained less error and, for instance, had a Chronbach alpha of .90..
.43 / sqrt(.83*.90)## [1] 0.4975173A much smaller difference. So this is what I mean when I say unreliability attenuates relationships. The more error there is in a measure, the smaller the relationship can be. It is therefore important to correct correlations for measurement error when we aggregate variables using psychological tools. And now you know how to!
Activity
For this activity, I want you to have a go at polynomial regression using the perfectionism dataset. To date, we have looked at the linear effect of perfectionism over time, but perhaps the trend is quadratic, or maybe cubic. Have a go at finding out.
Task 1 - Plot the relationship
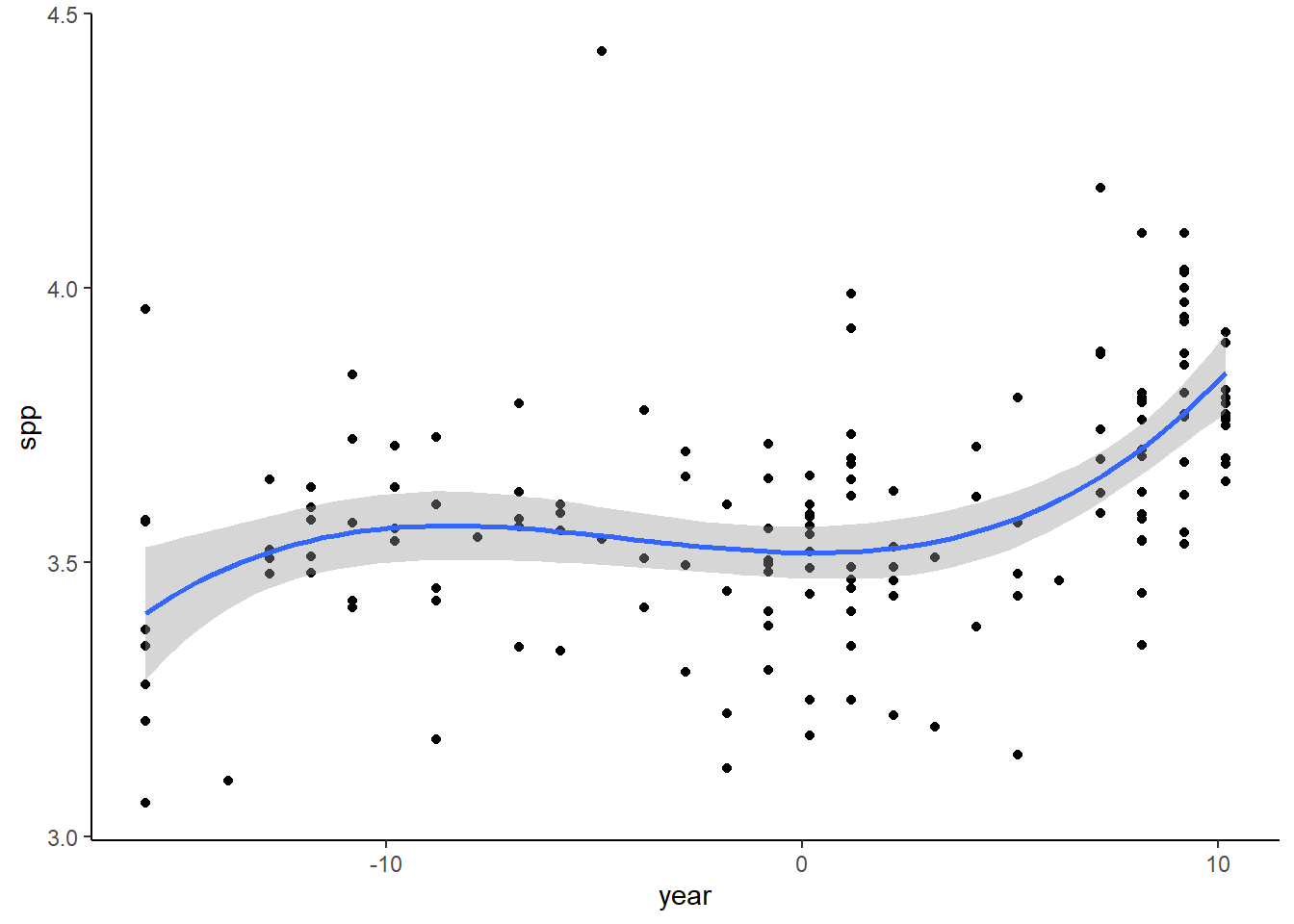
Use the chunk code below to plot the points for the relationship between year and spp in the perfectionism dataframe.
plot1 <- ggplot(perfectionism, aes(x = year, y = spp)) + geom_point() + theme_classic()
plot1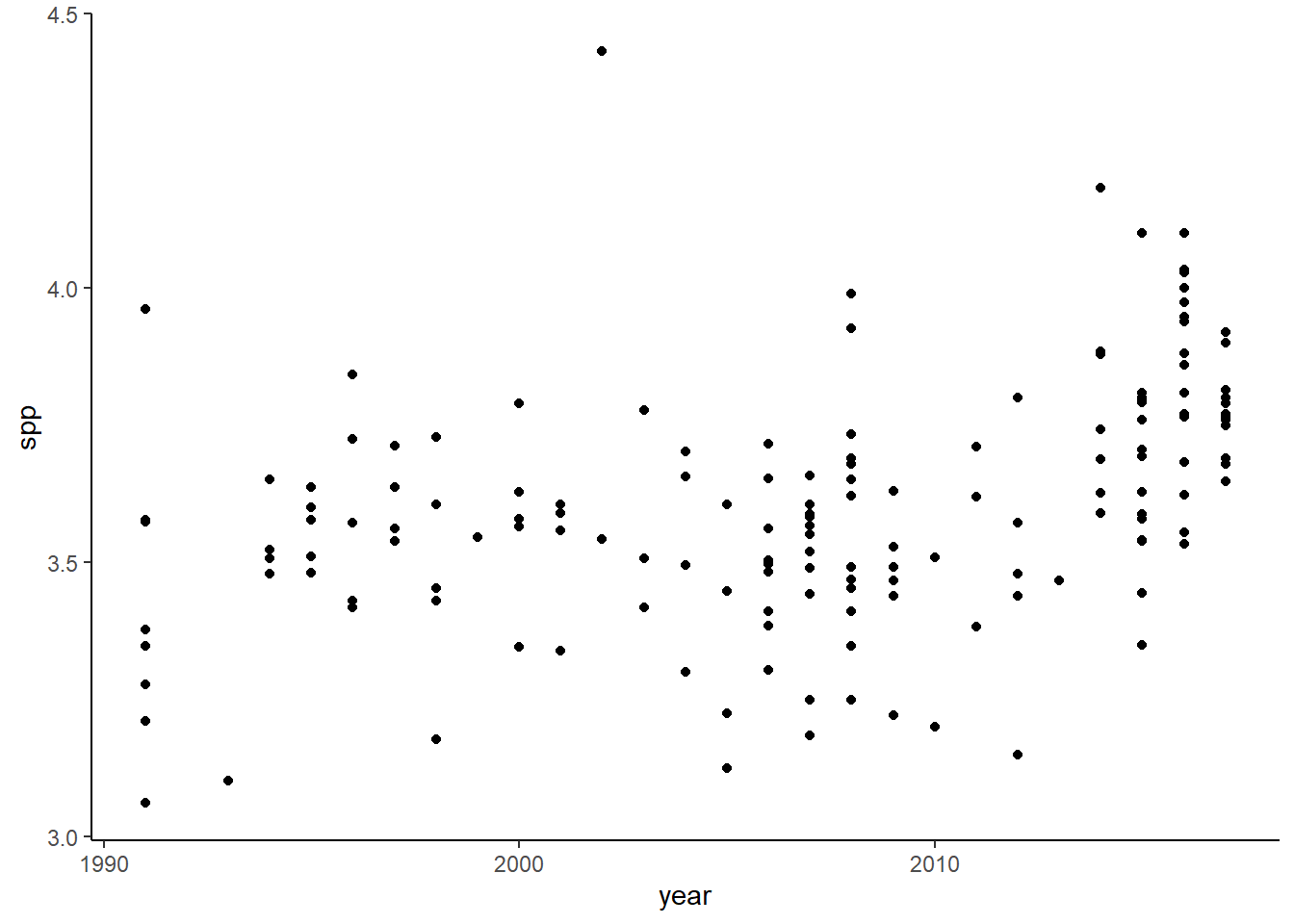
Describe the shape of this trend:
Task 2 - Mean center the predictor variable
Before we look at this relationship, we must center the predictor (year) at the mean. First lets calculate the mean for year.
mean(perfectionism$year)## [1] 2006.811And then subtract this mean from the observed year..
perfectionism$year <- (perfectionism$year-2006.811)
perfectionism## # A tibble: 159 x 4
## id year spp age
## <dbl> <dbl> <dbl> <dbl>
## 1 1 -15.8 3.58 25.4
## 2 2 -15.8 3.96 24.3
## 3 3 -15.8 3.06 22.1
## 4 4 -15.8 3.21 21
## 5 5 -15.8 3.35 19.9
## 6 6 -15.8 3.28 18.2
## 7 7 -15.8 3.57 18.6
## 8 8 -15.8 3.38 20
## 9 9 -13.8 3.10 22
## 10 10 -12.8 3.48 23
## # ... with 149 more rowsFinally, lets now plot the relationship with the centered year variable to make sure it hasn’t altered any other characteristics of the data
plot2 <- ggplot(perfectionism, aes(x = year, y = spp)) + geom_point() + theme_classic()
plot2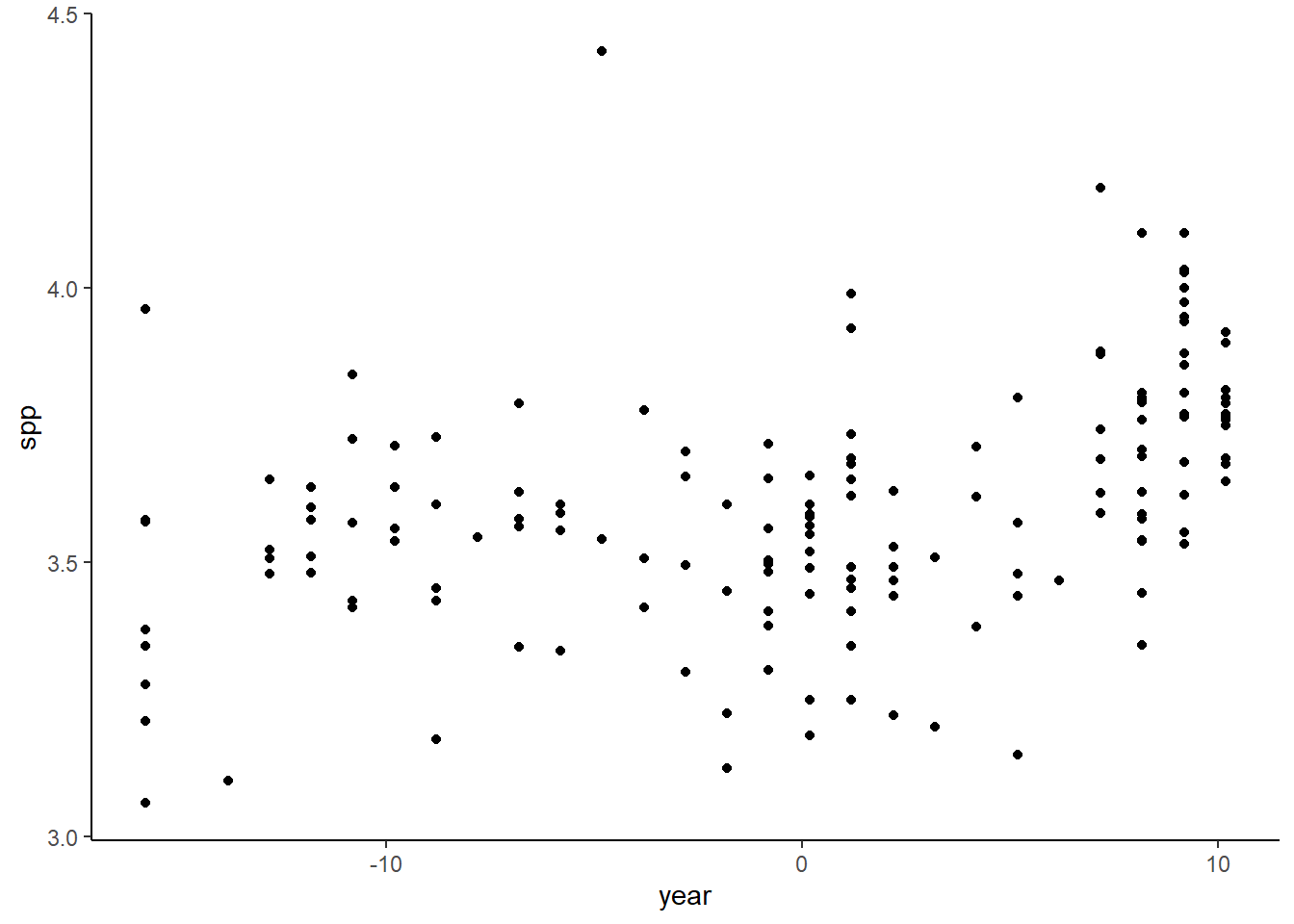
Task 3 - Test the linear model
First we need to test the linear model to ascertain if there is a linear trend. Lets build the linear model now and save it as a new R object called per1..
per1 <- lm(spp ~ year, data = perfectionism)
summary(per1)##
## Call:
## lm(formula = spp ~ year, data = perfectionism)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.50989 -0.12432 0.00529 0.10580 0.88624
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.600667 0.016138 223.122 < 2e-16 ***
## year 0.011412 0.002042 5.589 9.88e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2035 on 157 degrees of freedom
## Multiple R-squared: 0.1659, Adjusted R-squared: 0.1606
## F-statistic: 31.24 on 1 and 157 DF, p-value: 9.877e-08What is the R2 associated with this model?
What is the beta for year?
Is the beta significant?
Task 4 - Test the quadratic model
Next we need to test the quadratic model, with year raised to the 2nd power. To do this we just add year^2 to our linear model. Lets do that now and save it as a new R object called per2..
per2 <- lm(spp ~ year + I(year^2), data = perfectionism)
summary(per2)##
## Call:
## lm(formula = spp ~ year + I(year^2), data = perfectionism)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.49420 -0.11097 0.00312 0.10936 0.93229
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.5482883 0.0232424 152.665 < 2e-16 ***
## year 0.0141320 0.0021791 6.485 1.11e-09 ***
## I(year^2) 0.0008386 0.0002740 3.060 0.0026 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1983 on 156 degrees of freedom
## Multiple R-squared: 0.2132, Adjusted R-squared: 0.2031
## F-statistic: 21.13 on 2 and 156 DF, p-value: 7.562e-09What is the R2 associated with this model?
What is the beta for the quadratic effect?
Is the beta significant?
Now let’s see whether the introduction of the quadratic term improves the linear model using anova()..
anova(per1, per2)## Analysis of Variance Table
##
## Model 1: spp ~ year
## Model 2: spp ~ year + I(year^2)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 157 6.5010
## 2 156 6.1328 1 0.36816 9.3648 0.002605 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Does the addition of the quadratic term improve the model?
Why?
Test the cubic model
Finally we need to test the cubic model, with year raised to the 3rd power. To do this we just add year^3 to our quadratic model. Lets do that now and save it as a new R object called per3..
per3 <- lm(spp ~ year + I(year^2) + I(year^3), data = perfectionism)
summary(per3)##
## Call:
## lm(formula = spp ~ year + I(year^2) + I(year^3), data = perfectionism)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.43139 -0.11375 -0.00805 0.09348 0.88326
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.518e+00 2.392e-02 147.062 < 2e-16 ***
## year -1.061e-03 4.748e-03 -0.223 0.823477
## I(year^2) 1.788e-03 3.750e-04 4.768 4.25e-06 ***
## I(year^3) 1.454e-04 4.074e-05 3.569 0.000478 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1912 on 155 degrees of freedom
## Multiple R-squared: 0.2729, Adjusted R-squared: 0.2588
## F-statistic: 19.39 on 3 and 155 DF, p-value: 9.944e-11What is the R2 associated with this model?
What is the beta for the cubic effect?
Is the beta significant?
Now let’s see whether the introduction of the cubic term improves the quadratic model using anova()..
anova(per2, per3)## Analysis of Variance Table
##
## Model 1: spp ~ year + I(year^2)
## Model 2: spp ~ year + I(year^2) + I(year^3)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 156 6.1328
## 2 155 5.6672 1 0.46561 12.735 0.0004781 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Does the addition of the quadratic term improve the model?
Why?
Task 5 - Plot the trend
To visualize this relationship draw a figure that fits the best fitting shape to the data (i.e., linear, quadratic, or cubic). You can use the original plot1 from task 1 and add the stat_smooth layer with the best fitting polynomial model in the formula.
plot2 + stat_smooth(method = "lm", formula = y ~ x + I(x^2) + I(x^3), size = 1)